Question

Identify whether each equation has one solution, no solution, or infinitely many solutions.

9. 3 − x = x − 3
10. 4x − 8 = 4(x − 2)
11. 5(1 − x) = 5 + 5x
12. x + 2(x − 7) = 3x − 7

Answer 1

Problem 9: One solution

Problem 10: Infinitely many solutions

Problem 11: One solution

Problem 12: No solution

Explanation:

Solving one-variable equations

When solving a one variable equation, there are two steps:

• Step 1. Get the variable to show up exactly once
• Step 2. Get the variable by itself

During Step 1 of that process, usually one will be combining like-terms to take two terms that contain x, and merging them into one term that contains x. However, occasionally, the like terms contain x will completely cancel, leaving an equation with no variable left in it.

At that point, there are one of two possibilities:

• Possibility #1: The remaining equation is true
• Possibility #2: The remaining equation is false

If the remaining equation is true, it doesn't matter what the value of x is, the equation will be true. This means there are infinitely many solutions (any value of x will make the equation true).

Similarly, if the remaining equation is false, it doesn't matter what the value of x is, the equation will be false. This means there are no solutions (no values of x that will make the equation true).

Problem 9

`3-x=x-3`

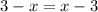
Add "x" to both sides to move the x-term on the left side of the equation from the left, to the right side, and group like terms.

`3=2x-3`

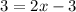
We were able to combine like terms containing the x into a single term. This equation will have one solution.

The remaining work is unnecessary to answer the question, but shows that there is one solution, the steps to find it, and what it is.

`6=2x`

`3=x`

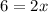
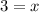
Problem 10

`4x-8=4(x-2)`

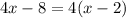
Use the distributive property on the expression on right hand side of the equation ...

`4x-8=4x-8`

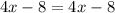
Observe that at this point, the entire left hand side of the equation EXACTLY matches that of the entire right hand side of the equation.

They are not just equal, they are exactly the same.

Attempting to move the term with x on the left hand side to the right hand side will require subtracting 4x from both sides, but combining like terms will cancel all terms with x on both sides....

`-8=-8`

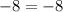
Since negative eight is ALWAYS equal to negative eight, no matter what value you choose for x, the equation must be true because each side is the same exact expression. This means there are infinitely many solutions.

Problem 11

`5(1-x)=5+5x`

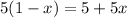
Apply the distributive property on the expression on left hand side of the equation ...

`5-5x=5+5x`

Add 5x to both sides of the equation to move the terms with x on the left side to the right side of the equation, and combine like terms...

`5=5+10x`

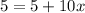
Again, we were able to combine like terms containing the x into a single term. This equation will have only one solution:

Subtract 5 from both sides...

`0=10x`

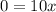
Divide both sides by 10...

`0=x`

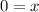
Problem 12

`x+2(x-7)=3x-7`

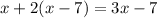
Apply the distributive property on the expression on left hand side of the equation ...

`x+2x-14=3x-7`

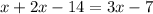
Combine like terms on the left hand side of the equation...

`3x-14=3x-7`

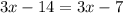
To move the term with x from the left side to the right side, subtract 3x from both sides, and combine like terms...

`-14=-7`

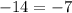
Here, when combining like terms, the x all canceled out, and negative 14 is not equal to negative 7. So, there is no solution so this equation.