Answer:
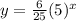 or
or
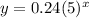
Explanation:
You know two points, so make two equations:
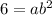
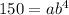
Solving for
 in the first equation, we have
in the first equation, we have
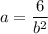 , so this value can be plugged into the second equation to solve for
, so this value can be plugged into the second equation to solve for
 :
:

Thus, we can now find the value of
 given that
given that
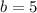 using either equation (I'll use the first one since it's easier):
using either equation (I'll use the first one since it's easier):
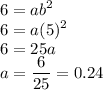
Hence, the exponential function whose graph passes through the given points is
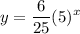 , or
, or
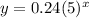 . I've attached a Desmos graph, and the regression confirms this answer is correct.
. I've attached a Desmos graph, and the regression confirms this answer is correct.