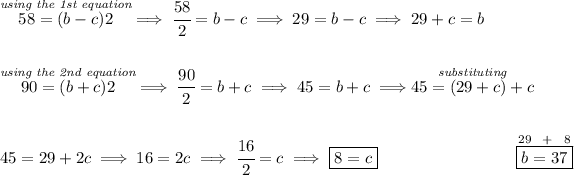Question

A motorboat travels 58 kilometers in 2 hours going upstream. It travels 90 kilometers going downstream in the same amount of time. What is the rate of the boat in still water and what is the rate of the current? km​

Answer 1

b = speed of the boat in still water

c = speed of the current

when going Upstream, the boat is not really going "b" fast, is really going slower, is going "b - c", because the current is subtracting speed from it, likewise, when going Downstream the boat is not going "b" fast, is really going faster, is going "b + c", because the current is adding its speed to it.

We also know it took 2 hours Upstream as well as Downstream, and we also know how far it went, so

`{\Large \begin{array}{llll} \underset{distance}{d}=\underset{rate}{r} \stackrel{time}{t} \end{array}} \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{lcccl} &\stackrel{km}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ \cline{2-4}&\\ Upstream&58&b-c&t\\ Downstream&90&b+c&t \end{array}\hspace{5em} \begin{cases} 58=(b-c)(2)\\\\ 90=(b+c)(2) \end{cases} \\\\[-0.35em] ~\dotfill`

`\stackrel{\textit{using the 1st equation}}{58=(b-c)2}\implies \cfrac{58}{2}=b-c\implies 29=b-c\implies 29+c=b \\\\\\ \stackrel{\textit{using the 2nd equation}}{90=(b+c)2}\implies \cfrac{90}{2}=b+c\implies 45=b+c\implies \stackrel{\textit{substituting}}{45=(29+c)+c} \\\\\\ 45=29+2c\implies 16=2c\implies \cfrac{16}{2}=c\implies \boxed{8=c}~\hfill \stackrel{ 29~~ + ~~8 }{\boxed{b=37}}`