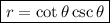Question

Convert the polar equation to rectangular form. and Convert the rectangular equation to polar form

please show or explain the steps of work so I can learn to do this myself

Answer 1

4)
`(x-1)^2 + (y - 1)^2 = 2`

Explanation:

4) We can convert this polar equation to rectangular form using the following formulas:

• 
  `r^2 = x^2 + y^2`
• 
  `r \sin(\theta) = y`
• 
  `r\cos(\theta) = x`
• 
  `\tan(\theta) = (y)/(x)`

We need to manipulate the equation so some of the terms match these formulas.

`r=2\cos(\theta) + 2\sin(\theta)`

↓ dividing both sides by
`2`

`r / 2=\cos(\theta) + \sin(\theta)`

↓ multiplying both sides by
`r`

`(r^2)/(2)=r\cos(\theta) + r\sin(\theta)`

Now, we can apply the polar conversion formulas to get the equation:

`(x^2 + y^2)/(2)=x + y`

This can be manipulated to get a circle standard form equation.

↓ multiplying both sides by 2

`x^2 + y^2=2x + 2y`

↓ completing the square for
`x`

↓ moving the x's to one side

`x^2 -2x=-y^2 + 2y`

↓ adding (-2/2)², or 1, to both sides

`x^2 -2x + 1=-y^2 + 2y + 1`

↓ factoring the perfect square

`(x-1)^2=-y^2 + 2y + 1`

↓ completing the square for
`y`

↓ factoring a (-1) out of the right side

`(x-1)^2=-1(y^2 - 2y - 1)`

↓ adding (-1)(+2) to both sides

`(x-1)^2 - 2=-1(y^2 - 2y - 1 + 2)`

↓ simplifying

`(x-1)^2 - 2=-1(y^2 - 2y + 1)`

↓ factoring the perfect square

`(x-1)^2 - 2=-(y - 1)^2`

↓ adding
`(y-1)^2` to both sides

`(x-1)^2 + (y - 1)^2 - 2 = 0`

↓ adding 2 to both sides

`\boxed{(x-1)^2 + (y - 1)^2 = 2}`

Answer 2

`\textsf{4)} \quad \textsf{A.}\;\;(x-1)^2+(y-1)^2=2`

`\textsf{5)} \quad \textsf{A.}\;\;r=\cot \theta \csc \theta`

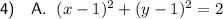
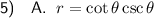
Explanation:

A polar equation is a mathematical expression that relates the distance (r) and angle (θ) of a point (r, θ) in a polar coordinate system.

Rectangular form, also known as Cartesian form, is a way of representing numbers or equations using the coordinates (x, y) in a Cartesian coordinate system. It is a standard way of expressing values in a two-dimensional space using the horizontal axis (x) and the vertical axis (y).

`\hrulefill`

Question 4

To convert a polar equation to rectangular form, we can use the following relationships:

`\boxed{\begin{aligned}r \cos \theta&=x\\\\r \sin \theta&=y\\\\r^2&=x^2+y^2\end{aligned}}`

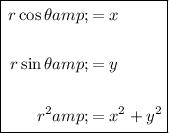
Given polar equation:

`r=2 \cos \theta+2 \sin \theta`

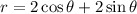
Multiply both sides of the equation by r:

`r^2=2r \cos \theta+2r \sin \theta`

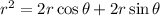
Substitute the expressions for r², r cosθ and r sinθ:

`x^2+y^2=2x+2y`

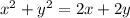
This is an equation of a circle.

To write it in standard form, move all the terms to the left side of the equation:

`x^2-2x+y^2-2y=0`

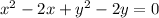
Add the square of half the coefficients of the x and y terms to both sides of the equation:

`x^2-2x+\left((-2)/(2)\right)^2+y^2-2y+\left((-2)/(2)\right)^2=0+\left((-2)/(2)\right)^2+\left((-2)/(2)\right)^2`

`x^2-2x+1+y^2-2y+1=2`

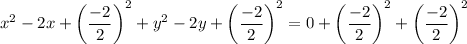
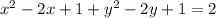
Factor the perfect square trinomials:

`(x^2-2x+1)+(y^2-2y+1)=2`

`(x-1)^2+(y-1)^2=2`

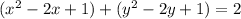
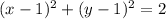
Therefore, the given polar form converted to rectangular form is:

`\boxed{(x-1)^2+(y-1)^2=2}`

`\hrulefill`

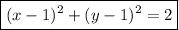
Question 5

To convert an equation in rectangular form to polar form, we can use the following relationships:

`\boxed{\begin{aligned}r \cos \theta&=x\\\\r \sin \theta&=y\\\\r^2&=x^2+y^2\end{aligned}}`

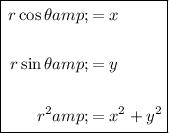
Given rectangular equation:

`x = y^2`

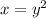
Substitute the expressions for x and y:

`r \cos \theta=(r \sin \theta)^2`

`r \cos \theta=r^2 \sin^2 \theta`

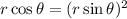
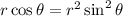
Divide both sides of the equation by r sin² θ:

`\begin{aligned}(r \cos \theta)/(r\sin^2 \theta)&=(r^2 \sin^2 \theta)/(r\sin^2 \theta)\\\\(\cos \theta)/(\sin^2 \theta)&=r\\\\r&=(\cos \theta)/(\sin^2 \theta)\\\\r&=(\cos \theta)/(\sin \theta)\cdot (1)/(\sin \theta)\end{aligned}`

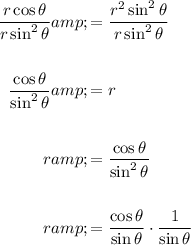
Use the following trigonometric identities to simplify:

`\boxed{\begin{minipage}{4 cm}\underline{Trigonometric Identities}\\\\$\cot \theta=(\cos \theta)/(\sin \theta)$\\\\\\$\csc \theta=(1)/(\sin \theta)$\\\end{minipage}}`

Therefore, the given rectangular form converted to polar form is:

`\boxed{r=\cot \theta \csc \theta}`