Question

Use property 8 to estimate the value of the integral.y tanxdx

Answer 1

The estimated value of the integral y = ∫tanx dx is y = -ln(cos(x)) + c

How to estimate the value of the integral.

From the question, we have the following parameters that can be used in our computation:

y = ∫tanx dx

This means that

`y = \int\limits {\tan(x)} \, dx`

Rewrite as

`y = \int\limits {(\sin(x))/(\cos(x)) \, dx`

Let u = cos(x)

So: du = -sin(x) dx

So, we have

`y = \int\limits {(-1)/(u) \, du`

Factor out the -1

`y = -\int\limits {(1)/(u) \, du`

Integrate

y = -ln(u) + c

Recall that

u = cos(x)

So, we have

y = -ln(cos(x)) + c

Hence, the estimated value of the integral is y = -ln(cos(x)) + c

Answer 2

The integral of
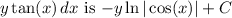`\(y \tan(x) \, dx\) is \(-y \ln|\cos(x)| + C\)`, where C is the constant of integration.

The integral
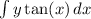`\(\int y \tan(x) \, dx\)` can be solved using integration by substitution.

Given the integral
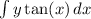`\(\int y \tan(x) \, dx\)`, let's use the substitution method where
`\(u = \cos(x)\) and \(du = -\sin(x) \, dx\)`.

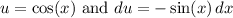Rewriting the integral in terms of u:

`\[ \int y \tan(x) \, dx = \int y (\sin(x))/(\cos(x)) \, dx = -y \int (1)/(u) \, du\]`

This simplifies to:

`\[ -y \int (1)/(u) \, du = -y \ln|u| + C = -y \ln|\cos(x)| + C\]`

Therefore, the solution to the integral
`\(\int y \tan(x) \, dx\) is \(-y \ln|\cos(x)| + C\)`, where C is the constant of integration.