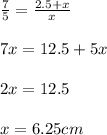Question

The diagram shows a triangle ACD. The line BE is parallel to the line CD. |BC| = 2.5 cm, |BE| = 5 cm, |CD|= 7 cm and |AB|= x cm. Work out the value of x.​

Answer 1

`x=6.25cm`

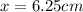
Explanation:

Given:

`BE/ /CD`

`BC=2.5cm`

`BE=5cm`

`CD=7cm`

`AB=x`

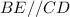
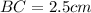
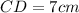
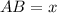
First, we need to prove that both triangles are similar in order to achieve something here we can go about that by using the fact that BE//CD:

since BE//CD, then:

`\angle ABF= \angle ACD\\\\\angle AEB=\angle ADC`

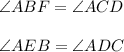
and since
`\angle A` is a common angle for both triangles, then both triangles are similar by AAA similarity.

Now, since both triangles are similar, we can use the ratio between their sides as a guide to get the length of the missing side:

`(7)/(5)=(2.5+x)/(x)\\ \\ 7x=12.5+5x\\\\2x=12.5\\\\x=6.25cm`