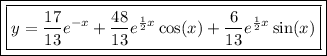Question

find the solution of the given initial value problem. (a computer algebra system is recommended.) 4y''' y' 5y = 0; y(0) = 5, y'(0) = 1, y''(0) = −1

Answer 1

`y=(17)/(13) e^(-x)+(48)/(13) e^{(1)/(2)x }\cos(x)+(6)/(13) e^{(1)/(2)x }\sin(x)`

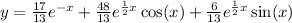
Explanation:

Given the third-order differential equation with initial conditions.

`4y'''+y'+5y=0; \ y(0)=5, \ y'(0)=1, \ y''(0)=-1`

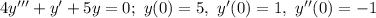
(1) - Find the characteristic equation

`4y'''+y'+5y=0\\\\\Longrightarrow 4m^3+0m^2+m+5=0\\\\\Longrightarrow \boxed{4m^3+m+5=0}`

(2) - Solve the characteristic equation for "m." First using the rational root theorem

`4m^3+m+5=0\\\\\rightarrow (p)/(q) = \pm (1,5)/(1,2,4) \\\\\text{\underline{Trying m=-1 first: }}\\\\ \begin{array}c\vphantom{\frac12}-1 & 4 & 0 & 1 & 5\\\cline{1-1} & \downarrow & -4 & 4 & -5\\\cline{2-5} & 4 & -4 & 5 & 0\end{array}\\\\\text{The remainder is 0} \ \therefore \boxed{m=-1} \ \text{is a root.}\\\\\text{Now we are left with}\rightarrow \boxed{4m^2-4m+5=0} \ \text{Use the quadratic equation}`

`\boxed{\left\begin{array}{ccc}\text{\underline{The Quadratic Equation:}}\\ax^2+bx+c=0\\\\x=(-b \pm√(b^2-4ac) )/(2a) \end{array}\right}`

`4m^2-4m+5=0\\\\\Longrightarrow m=(4 \pm√((-4)^2-4(4)(5)) )/(2(4)) \\\\\Longrightarrow m=(4 \pm√(-64) )/(8)\\\\\Longrightarrow m=(4)/(8) \pm (8i)/(8) \\\\\Longrightarrow \boxed{m=(1)/(2) \pm i}`

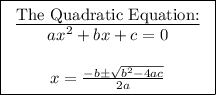
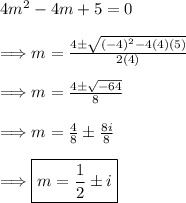
Thus, we have found three roots.

`m=-1, (1)/(2) \pm i`

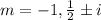
(3) - Form the solution.

`\boxed{\left\begin{array}{ccc}\text{\underline{Solutions to Higher-order DE's:}}\\\\\text{Real,distinct roots} \rightarrow y=c_1e^(m_1t)+c_2e^(m_2t)+...+c_ne^(m_nt)\\\\ \text{Duplicate roots} \rightarrow y=c_1e^(mt)+c_2te^(mt)+...+c_nt^ne^(mt)\\\\ \text{Complex roots} \rightarrow y=c_1e^(\alpha t)\cos(\beta t)+c_2e^(\alpha t)\sin(\beta t)+... \ ;m=\alpha \pm \beta i\end{array}\right}`

Notice that we have one real, distinct root and complex roots. Thus, we can form the solution in the following manner.

`\therefore \text{the general solution}\rightarrow\boxed{\boxed{y=c_1e^(-x)+c_2e^{(1)/(2)x }\cos(x)+c_3e^{(1)/(2)x }\sin(x)}}`

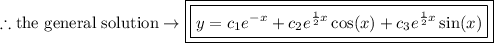
(4) - Use the given initial conditions to find the arbitrary constants "c_1," "c_2," and "c_3"

`\text{Recall...} \ y(0)=5, \ y'(0)=1, \ y''(0)=-1`

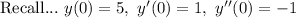
Take two derivatives of the general solution.

`y=c_1e^(-x)+c_2e^{(1)/(2)x }\cos(x)+c_3e^{(1)/(2)x }\sin(x)\\\\\\ \Rightarrow y'=-c_1e^(-x)+c_2(1)/(2)e^{(1)/(2)x}\cos(x)-c_2e^{(1)/(2)x}\sin(x)+c_3e^{(1)/(2)x }\cos(x)+c_3(1)/(2)e^{(1)/(2)x }\sin(x) \\\\\Longrightarrow \boxed{y'=-c_1e^(-x)+(c_3+(1)/(2) c_2)e^{(1)/(2)x}\cos(x)+(-c_2+(1)/(2) c_3)(3)/(2)e^{(1)/(2)x }\sin(x)}\\\\\\`

`\Rightarrow y''=c_1e^(-x)+(1)/(2) (c_3+(1)/(2) c_2)e^{(1)/(2)x }\cos(x)+(c_3+(1)/(2) c_2) e^{(1)/(2)x}sin(x)+(-c_2+(1)/(2) c_3)e^{(1)/(2)x } \cos(x)+(1)/(2) (-c_2+(1)/(2) c_3)e^{(1)/(2)x }\sin(x)\\\\\Longrightarrow \boxed{y''=c_1e^(-x)+(-(3)/(4) c_2+c_3)e^{(1)/(2)x }\cos(x)+(- c_2-(3)/(4)c_3) c_3e^{(1)/(2)x }\sin(x)}`

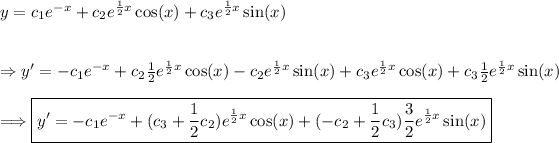
Plug in the initial conditions and form a system of equations.

`\left\{\begin{array}{ccc}5=c_1+c_2\\1=-c_1+(1)/(2)c_2+c_3 \\-1=c_1-(3)/(4)c_2+c_3 \end{array}\right`

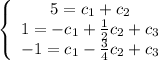
Creating a matrix and using a calculator to row-reduce,

`\Longrightarrow\left[\begin{array}{ccc}1&1&0\\-1&(1)/(2)&1\\1&-(3)/(4)&1\end{array}\right] =\left[\begin{array}{ccc}5\\1\\-1\end{array}\right] \\\\\Longrightarrow \left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right] =\left[\begin{array}{ccc}(17)/(13) \\(48)/(13) \\(6)/(13) \end{array}\right] \\\\\therefore \boxed{c_1=(17)/(13) , c_2=(48)/(13) , \ and \ c_3=(6)/(13) }`

(5) - Thus, the given differential equation is solved with the given initial conditions

`\boxed{\boxed{y=(17)/(13) e^(-x)+(48)/(13) e^{(1)/(2)x }\cos(x)+(6)/(13) e^{(1)/(2)x }\sin(x)}}`