Question

Test the series for convergence or divergence. [infinity] ∑ sin(9n) / 1+9^n n=1

Answer 1

Converges by Direct Comparison Test

Explanation:

For the infinite series
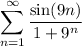`\displaystyle \sum^\infty_(n=1)(\sin(9n))/(1+9^n)`, we can use the direct comparison test. We need to check for absolute convergence, so let's assume
`\displaystyle \sum^\infty_(n=1)\biggr|(\sin(9n))/(1+9^n)\biggr|\leq\sum^\infty_(n=1)(1)/(1+9^n)`. Since
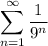`\displaystyle \sum^\infty_(n=1)(1)/(9^n)` is a geometric series with
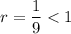`\displaystyle r=(1)/(9) < 1`, then that series converges. This implies that
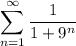`\displaystyle \sum^\infty_(n=1)(1)/(1+9^n)` converges, and so
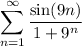`\displaystyle \sum^\infty_(n=1)(\sin(9n))/(1+9^n)` converges by the direct comparison test.