Question

Help is really appreciated
`a_n=3(0.25)^2^n^-^5`!

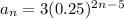
Mateo has worked for the same company for 6 years, and each year he gets a raise of $1,500. In the 6 years Mateo has worked for this company, he has earned a total of $208,500. What was Mateo’s pay for his first year?
$28,000
$30,000
$29,000
$31,000


An arithmetic series is defined by the formula
`a_n=2n+1`
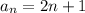
a) What is the first term of the series?
b) Write an expression for the sum of the first n terms of the series.

Given the following geometric series, find
`S_9`
12+6+3+...

S9=1533/64
S9=1533/2
S9=1533/8
S9=1533/4

The sum of an infinite series is 24, and the common ratio is 0.5. What is the first term of the series?

A sequence is defined by
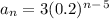
`a_n=3(0.2)^n^-^5`. Determine if its geometric or arithmetic and whether this sequence will converge or diverge.

The terms of an infinite geometric series are given by .

Show all work to find:
a) the first term of the series.
b) the common ratio of the series, rounded to four decimal places if necessary.
c) the sum of the series, rounded to the nearest hundredth if necessary.

The sum of an infinite series is given by
`S=(25)/(1+(3)/(4) )`. What is the common ratio of this series?
1
3/4
25
-3/4

Answer 1

a) To find the first term, plug in n=1 into the formula provided:

a = 4

b) To find the common ratio, use the formula provided:

r = -1/4

c) To find the sum of the series, use the formula for an infinite geometric series:

S = a/(1-r)

S = 4/(1-(-1/4)) = 16/3 = 5.33 (rounded to the nearest hundredth)

As for the second question,

The sum of an infinite series is given by

The formula for the sum of an infinite geometric series is:

S = a/(1-r)

where a is the first term and r is the common ratio.

The sum is equal to 25. Therefore:

25 = 1/(1-r)

Solving for r, we get:

r = -3/4