Question

use heron's formula to find the area of the triangle with side lengths 11, 15, and 19, as shown below.

Answer 1

• 82.41 square units

-------------------

Heron's formula states that the area of a triangle with side lengths a, b, and c is:

• 
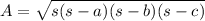  `A= √(s(s-a)(s-b)(s-c))`, where s = (a + b + c)/2 s is the semi-perimeter of the triangle.

We have a triangle with side lengths:

• a = 11, b = 15, and c = 19.

We can first find the semi-perimeter:

• s = (a + b + c)/2
• s = (11 + 15 + 19)/2
• s = 22.5

Then we can plug this into Heron's formula to find the area:

• 
  `A=√(22.5(22.5-11)(22.5-15)(22.5-19)) =√(6792.1875) =82.41\ rounded`

So the area of the triangle is approximately 82.41 square units.