Question

Let r be the separation vector from a fixed point (x’, y’, z’) to the point (x, y, z), and let r be its length. That is

Answer 1

(a) Refer to part (a)

(b) Refer to part (b)

(c)
`nr^(n-1)\bold{\hat{r}}`

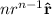
Explanation:

To answer the questions, I will show the derivations of each part by applying vector calculus methods such as the gradient operator, denoted by '▽', to the given quantities. I will use the definition of the gradient operator in Cartesian coordinates to solve each part.

Given:

`\bold{r} = (x-x')\hat{\imath}+ (y-y')\hat{\jmath} + (z-z')\hat{k}; \ r=√( (x-x')^2+(y-y')^2+(z-z')^2)`

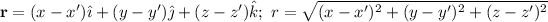
Show that:

(a)
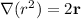
`\\abla (r^2)=2 \bold{r}`

(b)
`\\abla (1/r)=- \bold{\hat{r}}/r^2`

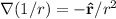
(c) What is the general formula for
`\\abla (r^n)`?

`\hrulefill`

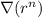Part (a): Proving
`\Large{\\abla (r^2)=2\hat{r}}`
`\hrulefill`

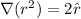
The gradient operator in Cartesian coordinates is:

`\\abla = \hat{\imath}(\partial)/(\partial x)+ \hat{k}(\partial)/(\partial y)+ \hat{\jmath}(\partial)/(\partial z)`

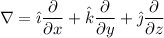
The square of the vector length is given by:

`\Longrightarrow r^2 = [(x-x')\hat{\imath}+ (y-y')\hat{\jmath} + (z-z')\hat{k}]^2\\\\\\\\\Longrightarrow r^2 = (x-x')^2\hat{\imath}+ (y-y')^2\hat{\jmath} + (z-z')^2\hat{k}`

Now, applying the gradient operator to 'r²':

`\Longrightarrow \\abla r^2 = \\\\\bullet (\partial)/(\partial x)[(x-x')^2\hat{\imath}+ (y-y')^2\hat{\jmath} + (z-z')^2\hat{k}]=2(x-x')\\\\\bullet (\partial)/(\partial y)[(x-x')^2\hat{\imath}+ (y-y')^2\hat{\jmath} + (z-z')^2\hat{k}] = 2(y-y')\\\\\bullet(\partial)/(\partial z)[(x-x')^2\hat{\imath}+ (y-y')^2\hat{\jmath} + (z-z')^2\hat{k}] =2(z-z')\\\\\\\\\therefore \\abla r^2=2(x-x')\hat{\imath}+ 2(y-y')\hat{\jmath} + 2(z-z')\hat{k}\\\\\\\\`

Factoring out a 2:

`\Longrightarrow \\abla r^2=2[(x-x')\hat{\imath}+ (y-y')\hat{\jmath} + (z-z')\hat{k}]\\\\\\\\\therefore \boxed{\\abla r^2=2 \bold{r}}`

`\hrulefill`

Part (b): Proving
`\\abla (1/r)=- \bold{\hat{r}}/r^2`
`\hrulefill`

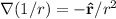
The length 'r' is given by:

`r=√( (x-x')^2+(y-y')^2+(z-z')^2)`

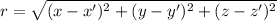
Now applying the gradient operator to 1/r:

`(1)/(r)=((x-x')^2+(y-y')^2+(z-z')^2)^(-1/2)`

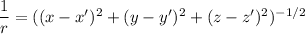
`\\abla (1)/(r) =\\\\\bullet (\partial)/(\partial x)[((x-x')^2+(y-y')^2+(z-z')^2)^(-1/2)]=-(x-x')[(x-x')^2+(y-y')^2+(z-z')^2]^(-3/2)\\\\\bullet(\partial)/(\partial y)[((x-x')^2+(y-y')^2+(z-z')^2)^(-1/2)]=-(y-y')[(x-x')^2+(y-y')^2+(z-z')^2]^(-3/2) \\\\\bullet(\partial)/(\partial z)[((x-x')^2+(y-y')^2+(z-z')^2)^(-1/2)]=-(z-z')[(x-x')^2+(y-y')^2+(z-z')^2]^(-3/2)`

`\Longrightarrow \\abla (1)/(r) = - \frac{(x-x')\hat{\imath}+ (y-y')\hat{\jmath} + (z-z')\hat{k}}{[(x-x')^2+ (y-y')^2 + (z-z')^2]^(3/2)}`

`\Longrightarrow \\abla (1)/(r) = -\frac{\bold{r}}{r^3}; \ \text{Where:} \ \bold{\hat{r}} =\frac{\bold{r}}{r} \rightarrow \bold{r}=\bold{\hat{r}}\cdot r \\\\\\\\\Longrightarrow \\abla (1)/(r) = -\frac{ \bold{\hat{r}} \cdot r}{r^3}\\\\\\\\\therefore \boxed{\\abla (1)/(r) = \frac{\bold{-\hat{r}}}{r^2}}`

`\hrulefill`

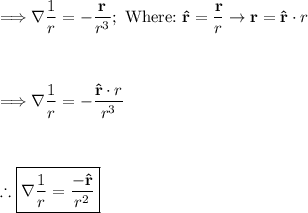
Part (c): General formula for
`\\abla (r^n)`
`\hrulefill`

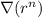
The general formula is as follows:

`\Longrightarrow \\abla(r^n)=(\partial)/(\partial r)[r^n] \bold{\hat{r}} \\\\\\\\\therefore \boxed{\\abla(r^n)=nr^(n-1)\bold{\hat{r}}}`