Answer:
(a) Refer to part (a)
(b) Refer to part (b)
(c)

Explanation:
To answer the questions, I will show the derivations of each part by applying vector calculus methods such as the gradient operator, denoted by '▽', to the given quantities. I will use the definition of the gradient operator in Cartesian coordinates to solve each part.
Given:
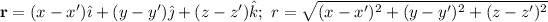
Show that:
(a)
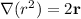
(b)
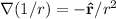
(c) What is the general formula for
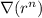 ?
?

Part (a): Proving
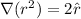

The gradient operator in Cartesian coordinates is:
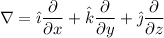
The square of the vector length is given by:
![\Longrightarrow r^2 = [(x-x')\hat{\imath}+ (y-y')\hat{\jmath} + (z-z')\hat{k}]^2\\\\\\\\\Longrightarrow r^2 = (x-x')^2\hat{\imath}+ (y-y')^2\hat{\jmath} + (z-z')^2\hat{k}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/q8eiswhseh21yjit4ayh.png)
Now, applying the gradient operator to 'r²':
![\Longrightarrow \\abla r^2 = \\\\\bullet (\partial)/(\partial x)[(x-x')^2\hat{\imath}+ (y-y')^2\hat{\jmath} + (z-z')^2\hat{k}]=2(x-x')\\\\\bullet (\partial)/(\partial y)[(x-x')^2\hat{\imath}+ (y-y')^2\hat{\jmath} + (z-z')^2\hat{k}] = 2(y-y')\\\\\bullet(\partial)/(\partial z)[(x-x')^2\hat{\imath}+ (y-y')^2\hat{\jmath} + (z-z')^2\hat{k}] =2(z-z')\\\\\\\\\therefore \\abla r^2=2(x-x')\hat{\imath}+ 2(y-y')\hat{\jmath} + 2(z-z')\hat{k}\\\\\\\\](https://img.qammunity.org/qa-images/2023/formulas/physics/college/xai82u088awmlatteold.png)
Factoring out a 2:
![\Longrightarrow \\abla r^2=2[(x-x')\hat{\imath}+ (y-y')\hat{\jmath} + (z-z')\hat{k}]\\\\\\\\\therefore \boxed{\\abla r^2=2 \bold{r}}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/kj3x6k8t1uts4osr71ux.png)

Part (b): Proving
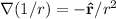

The length 'r' is given by:
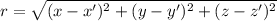
Now applying the gradient operator to 1/r:

![\\abla (1)/(r) =\\\\\bullet (\partial)/(\partial x)[((x-x')^2+(y-y')^2+(z-z')^2)^(-1/2)]=-(x-x')[(x-x')^2+(y-y')^2+(z-z')^2]^(-3/2)\\\\\bullet(\partial)/(\partial y)[((x-x')^2+(y-y')^2+(z-z')^2)^(-1/2)]=-(y-y')[(x-x')^2+(y-y')^2+(z-z')^2]^(-3/2) \\\\\bullet(\partial)/(\partial z)[((x-x')^2+(y-y')^2+(z-z')^2)^(-1/2)]=-(z-z')[(x-x')^2+(y-y')^2+(z-z')^2]^(-3/2)](https://img.qammunity.org/qa-images/2023/formulas/physics/college/fgoakzzp53fdl8bs6z2y.png)
![\Longrightarrow \\abla (1)/(r) = - \frac{(x-x')\hat{\imath}+ (y-y')\hat{\jmath} + (z-z')\hat{k}}{[(x-x')^2+ (y-y')^2 + (z-z')^2]^(3/2)}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/2bq0f1kd1cap8cfd4ig7.png)
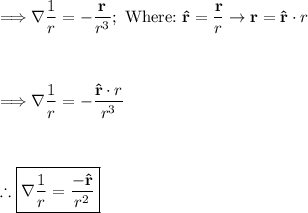

Part (c): General formula for
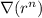

The general formula is as follows:
![\Longrightarrow \\abla(r^n)=(\partial)/(\partial r)[r^n] \bold{\hat{r}} \\\\\\\\\therefore \boxed{\\abla(r^n)=nr^(n-1)\bold{\hat{r}}}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/427nfa3xj8qjhu8v8sk5.png)