Question

A gas in a cylinder is held at a constant pressure of 1.8×105 Pa and is heated and expanded from 1.2 m3 to 1.7 m3. What is the work done by (or on) the gas?

a. 5.2×105 J done by the system
b. 9.0×104 J done on the system
c. 9.0×104 J done by the system
d. 5.2×105 J done on the system

Answer 1

`W_(by)=9.00 * 10^4 \ J\\\\W_(on)=-9.00 * 10^4 \ J`

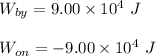
Option (c) is correct.

Step-by-step explanation:

`\boxed{\left\begin{array}{ccc}\text{\underline{Work done on/by a gas:}}\\W_(by)=P \Delta V \ or \ \int\limits^(V_f)_(V_0) {P} \, dV \\W_(on)=-P\Delta V \ or \ -\int\limits^(V_f)_(V_0) {P} \, dV \end{array}\right }`

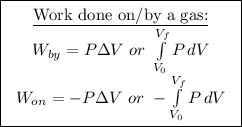
Given:

`P=1.8 * 10^5 \ Pa\\\\V_0=1.2 \ m^3\\\\V_f=1.7 \ m^3`

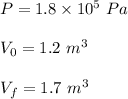
Find:

`W_(by)=?? \ J\\\\W_(on)=?? \ J`

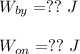
(1) - Calculating the change in volume

`\Delta V= V_f-V_0\\\\\Longrightarrow \Delta V=1.7-1.2\\\\\therefore \boxed{\Delta V=0.5 \ m^3}`

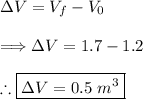
(2) - Calculating the work done by the gas

`W_(by)=P \Delta V\\\\\Longrightarrow W_(by)=(1.8 * 10^5)(0.5)\\\\\therefore \boxed{\boxed{W_(by)=9.00 * 10^4 \ J}}`

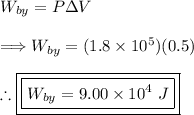
(3) - Calculating the work done on the gas

`W_(on)=-P \Delta V\\\\\Longrightarrow W_(on)=-(1.8 * 10^5)(0.5)\\\\\therefore \boxed{\boxed{W_(on)=-9.00 * 10^4 \ J}}`

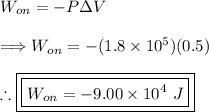
Options (a) and (d) can be eliminated. Option (b) can be eliminated since there is no negative in front of the answer. This leaves the correct answer being option (c).