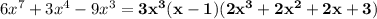Question

6x^7+3x^4-9x^3 factor

Answer 1

`3x^3(x-1)(2x^3+2x^2+2x+3)`

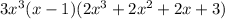
Explanation:

We can start by factoring out x³ because it's the greatest factor of every term:

`6x^7+3x^4-9x^3=x^3(6x^4+3x-9)`

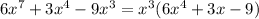
Next, notice that each coefficient is divisible by 3, so this can be factored out as well:

`x^3(6x^4+3x-9)=3x^3(2x^4+x-3)`

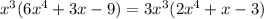
While it may not look like we can factor out 2x⁴+x-3, we actually can! Notice the following:

`2x^4+x-3=(2x^4+2x^3+2x^2+3x)+(-2x^3-2x^2-2x-3)=x(2x^3+2x^2+2x+3)-1(2x^3-2x^2+2x+3)=(x-1)(2x^3+2x^2+2x+3)`

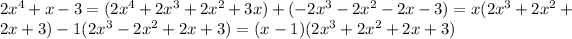
By grouping, we were able to condense this factor. Thus:

`6x^7+3x^4-9x^3=\bf{3x^3(x-1)(2x^3+2x^2+2x+3)}`