Answer:
Length is approximately 7.073 m
Explanation:
One of the formulas we can use for surface area of a triangular prism is:
SA = bh + L(s1 + s2 + s3), where
- SA is the surface area in square units,
- b is the base of the triangle,
- h is the height of the triangle,
- L is the length of the prism (i.e., side connecting two triangles),
- and s1, s2, and s3 are the three sides of the triangle
So far, we know that the surface area is 297 and the height is 8.7.
Step 1: We see that the line indicating the height splits the larger triangle into two right triangles, Thus, we can find the base of one of the right triangles using the Pythagorean theorem and multiply this by 2 to find the measure of the entire base.
The Pythagorean theorem is:
a^2 + b^2 = c^2, where
- a and b are the shorter legs,
- and c is the longest leg, known as the hypotenuse (always opposite the right angle)
We have the measure of one leg (8.7 m) and the hypotenuse (10 m) and we must solve for leg:
a^2 + 8.7^2 = 10^2
a^2 + 75.69 = 100
a^2 = 24.31
a = √24.31 m
Multiplying this by 2 gives us that the measure of the entire base is 2√24.31 m.
Step 2: Now we can plug in 297 for sa, 2√24.31 for b, 8.7 for h, and 10, 10, and 2√24.31 for s1, s2, and s3 respectively. This will allow us to solve for L, the length of the triangular prism:
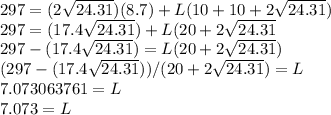
Thus, the length of the missing side is approximately 7.073 m
Optional Step 3: We can check that we've found the correct length of the missing side by plugging in 7.073 for L in the surface area formula and checking that we get 297 (or at least something very close to it):
297 = (2√24.31)(8.7) + 7.073(10 + 10 + 2√24.31)
297 = (17.4√24.31) + 7.073(20 + 2√24.31)
297 = (17.4√24.31) + 141.46 + 14.146√24.31
297 > 296.998096
You get approximately the same answer since we rounded the length to the nearest thousandth. If you were to plug in a more exact answer like ((297 - (17.4√24.31)) / (20 + 2√24.31) for L, you'd get exactly 297 as I plugged this in for L on my TI-84 and got 297 exactly.