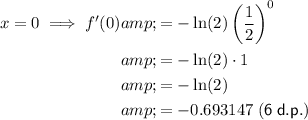Question

(question 7) calculus

Answer 1

A. -0.693147

Explanation:

Replace f(x) with y in the given function:

`y=\left((1)/(2)\right)^x`

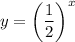
Take natural logs of both sides of the equation:

`\ln y=\ln \left((1)/(2)\right)^x`

`\textsf{Apply the log power law:} \quad \ln a^n=n \ln a`

`\ln y=x\ln \left((1)/(2)\right)`

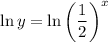
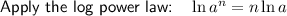
Differentiate using implicit differentiation.

Place d/dx in front of each term of the equation:

`\frac{\text{d}}{\text{d}x}\ln y=\frac{\text{d}}{\text{d}x}x\ln \left((1)/(2)\right)`

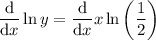
Differentiate with respect to x:

`(1)/(y) \frac{\text{d}y}{\text{d}x}=\ln \left((1)/(2)\right)`

`\textsf{Apply the log quotient law:} \quad \ln \left((a)/(b)\right) = \ln a - \ln b`

`(1)/(y) \frac{\text{d}y}{\text{d}x}=\ln(1)-\ln(2)`

`(1)/(y) \frac{\text{d}y}{\text{d}x}=0-\ln(2)`

`(1)/(y) \frac{\text{d}y}{\text{d}x}=-\ln(2)`

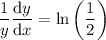
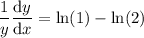
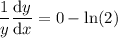
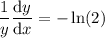
Multiply both sides by y:

`\frac{\text{d}y}{\text{d}x}=-y\ln (2)`

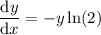
Substitute back in the expression for y:

`\frac{\text{d}y}{\text{d}x}=-\left((1)/(2)\right)^x\ln (2)`

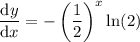
Therefore, the differentiated function is:

`f'(x)=-\ln(2)\left((1)/(2)\right)^x`

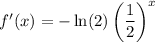
To find f'(0), substitute x = 0 into the differentiated function:

`\begin{aligned}x=0 \implies f'(0)&=-\ln(2) \left((1)/(2)\right)^0\\&=-\ln(2) \cdot 1\\&=-\ln(2) \\&=-0.693147\; \sf (6\;d.p.)\end{aligned}`