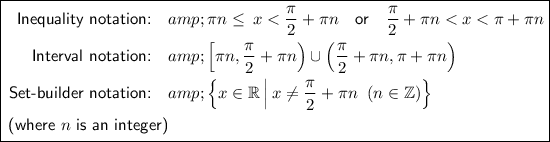Question

PLEASE HELPPP!!!!SOMEONEEEE

Answer 1

(i) x ≤ 1

(ii) ℝ except 0, -1

(iii) x > -1

(iv) ℝ except π/2 + nπ, n ∈ ℤ

Explanation:

(i) The number inside a square root must be positive or zero to give the expression a real value. Therefore, to solve for the domain of the function, we can set the value inside the square root greater or equal to 0, then solve for x:

`1-x \ge 0`

`1 \ge x`

`\boxed{x \le 1}`

(ii) The denominator of a fraction cannot be zero, or else the fraction is undefined. Therefore, we can solve for the values of x that are NOT in the domain of the function by setting the expression in the denominator to 0, then solving for x.

`0 = x^2+x`

`0 = x(x + 1)`

`x = 0` OR
`x = -1`

So, the domain of the function is:

`R \text{ except } 0, -1`

(ℝ stands for "all real numbers")

(iii) We know that the value inside a logarithmic function must be positive, or else the expression is undefined. So, we can set the value inside the log greater than 0 and solve for x:

`x+ 1 > 0`

`\boxed{x > -1}`

(iv) The domain of the trigonometric function tangent is all real numbers, except multiples of π/2, when the denominator of the value it outputs is zero.

`\boxed{R \text{ except } \frac{\pi}2 + n\pi} \ \text{where} \ \text{n} \in Z`

(ℤ stands for "all integers")

Answer 2

(i) x ≤ 1

(ii) All real numbers except x = 0 and x = -1.

(iii) x > -1

(iv) All real numbers except x = π/2 + πn, where n is an integer.

Explanation:

What is the domain?

The domain of a function is the set of all possible input values (x-values).

`\hrulefill`

`\textsf{(i)} \quad f(x)=√(1-x)`

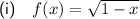
For a square root function, the expression inside the square root must be non-negative. Therefore, for function f(x), 1 - x ≥ 0.

Solve the inequality:

`\begin{aligned}1 - x &\geq 0\\\\1 - x -1 &\geq 0-1\\\\-x &\geq -1\\\\(-x)/(-1) &\geq (-1)/(-1)\\\\x &\leq 1\end{aligned}`

(Note that when we divide or multiply both sides of an inequality by a negative number, we must reverse the inequality sign).

Hence, the domain of f(x) is all real numbers less than or equal to -1.

`\boxed{\begin{aligned} \textsf{Inequality notation:} \quad &x \leq 1\\\textsf{Interval notation:} \quad &(-\infty, 1]\\\textsf{Set-builder notation:} \quad &\left\{x \in \mathbb{R}\left|\: x \leq 1 \right\} \end{aligned}}`

`\hrulefill`

`\textsf{(ii)} \quad g(x) = (1)/(x^2 + x)`

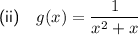
To find the domain of g(x), we need to identify any values of x that would make the denominator equal to zero, since division by zero is undefined.

Set the denominator to zero and solve for x:

`\begin{aligned}x^2 + x &= 0\\x(x + 1) &= 0\\\\\implies x &= 0\\\implies x &= -1\end{aligned}`

Therefore, the domain of g(x) is all real numbers except x = 0 and x = -1.

`\boxed{\begin{aligned} \textsf{Inequality notation:} \quad &x < -1 \;\;\textsf{or}\;\; -1 < x < 0 \;\;\textsf{or}\;\; x > 0\\\textsf{Interval notation:} \quad &(-\infty, -1) \cup (-1, 0) \cup (0, \infty)\\\textsf{Set-builder notation:} \quad &\left\{x \in \mathbb{R}\left|\: x \\eq 0,x \\eq -1 \right\} \end{aligned}}`

`\hrulefill`

`\textsf{(iii)}\quad h(x) = \log_7(x + 1)`

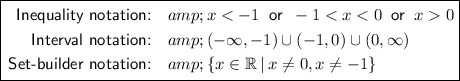
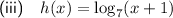
For a logarithmic function, the argument (the expression inside the logarithm), must be greater than zero.

Therefore, for function h(x), x + 1 > 0.

Solve the inequality:

`\begin{aligned}x + 1 & > 0\\x+1-1& > 0-1\\x & > -1\end{aligned}`

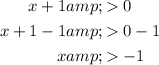
Therefore, the domain of h(x) is all real numbers greater than -1.

`\boxed{\begin{aligned} \textsf{Inequality notation:} \quad &x > -1\\\textsf{Interval notation:} \quad &(-1, \infty)\\\textsf{Set-builder notation:} \quad &\left\{x \in \mathbb{R}\left|\: x > -1\right\} \end{aligned}}`

`\hrulefill`

`\textsf{(iv)} \quad k(x) = \tan x`

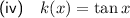
The tangent function can also be expressed as the ratio of the sine and cosine functions:

`\tan x = (\sin x)/(\cos x)`

Therefore, the tangent function is defined for all real numbers except the values where the cosine of the function is zero, since division by zero is undefined.

From inspection of the unit circle, cos(x) = 0 when x = π/2 and x = 3π/2.

The tangent function is periodic with a period of π. This means that the graph of the tangent function repeats itself at intervals of π units along the x-axis.

Therefore, if we combine the period and the undefined points, the domain of k(x) is all real numbers except x = π/2 + πn, where n is an integer.

`\boxed{\begin{aligned} \textsf{Inequality notation:} \quad &\pi n\le \:x < (\pi )/(2)+\pi n\quad \textsf{or}\quad (\pi )/(2)+\pi n < x < \pi +\pi n\\\textsf{Interval notation:} \quad &\left[\pi n ,(\pi )/(2)+\pi n\right) \cup \left((\pi )/(2)+\pi n,\pi +\pi n\right)\\\textsf{Set-builder notation:} \quad &\left\{x \in \mathbb{R}\left|\: x \\eq (\pi)/(2)+\pi n\;\; (n \in\mathbb{Z}) \right\}\\\textsf{(where $n$ is an integer)}\end{aligned}}`