Question

A line contains the points R (-5, -6) S (1, 5) and T (x, 10). Solve for x. Be sure to show and explain all work.

Per my son's teacher we need to find the slope of the first 2 points and then use the slope formula with that slope and the x and y values of Point T to find x.

Answer 1

well, that's correct, hmmmm so let's check for the slope of RS

`R(\stackrel{x_1}{-5}~,~\stackrel{y_1}{-6})\qquad S(\stackrel{x_2}{1}~,~\stackrel{y_2}{5}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{5}-\stackrel{y1}{(-6)}}}{\underset{\textit{\large run}} {\underset{x_2}{1}-\underset{x_1}{(-5)}}} \implies \cfrac{5 +6}{1 +5} \implies \cfrac{ 11 }{ 6 } \implies \cfrac{11}{6}`

since all three points are collinear, that means that they all share the same slope, so the slope for ST must also be the same RS has, thus

`S(\stackrel{x_1}{1}~,~\stackrel{y_1}{5})\qquad T(\stackrel{x_2}{x}~,~\stackrel{y_2}{10}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{10}-\stackrel{y1}{5}}}{\underset{\textit{\large run}} {\underset{x_2}{x}-\underset{x_1}{1}}} ~~ = ~~\stackrel{\stackrel{\textit{\small slope}}{\downarrow }}{ \cfrac{ 11 }{ 6 }}\implies \cfrac{5}{x-1}=\cfrac{11}{6}\implies 30=11x-11 \\\\\\ 41=11x\implies \cfrac{41}{11}=x`

Answer 2

Answer: The coordinates of point T are approximately (3.73, 10).

Explanation:

Your son's teacher is correct. In this case, we can use the formula for the slope of a line, which is defined as the change in y-values (vertical difference) divided by the change in x-values (horizontal difference) between two points

Let's start by finding the slope between points R and S. The coordinates for these points are R(-5, -6) and S(1, 5) respectively

The formula for the slope (m) is:

`m = (y2 - y1) / (x2 - x1)`

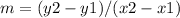
Substituting the coordinates of points R and S into the formula gives:

`m = (5 - (-6)) / (1 - (-5)) = 11 / 6`

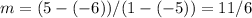
So, the slope between points R and S is 11/6.

Now, we know that the slope between points S and T should be the same because they are on the same line. The coordinates for these points are S(1, 5) and T(x, 10)

Using the same slope formula, we set the slope to be the same as the slope we found earlier (11/6):

`11/6 = (10 - 5) / (x - 1)`

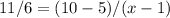
This simplifies to:

`11/6 = 5 / (x - 1)`

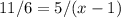
To solve for x, we can cross-multiply and solve the resulting equation:

`11 * (x - 1) = 6 * 5`

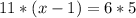
This gives:

`11x - 11 = 30`

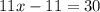
Adding 11 to both sides gives:

`11x = 41`

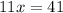
Finally, dividing both sides by 11 gives the x-coordinate of point T:

`x = 41 / 11`

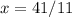
So, x = 3.73 (rounded to two decimal places).

Therefore, the coordinates of point T are approximately (3.73, 10).