Question

Solve
`3xlog 2+log8^x=2`

Answer 1

Hello !

Answer:

`\boxed{\sf x = (1)/( log(8) ) }`

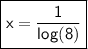
Explanation:

We want to find the value of x that verifies the following equation :

`\sf 3xlog 2+log(8^x)=2`

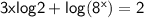
Let's remember :

`\sf log( {x}^(a) ) = a * log(x)`

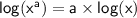
We can apply this property to our equation :

`\sf 3x log(2 ) + x log(8) = 2`

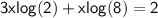
Let's factor the left side by x :

`\sf x(3 log(2) + log(8) ) = 2`

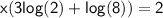
We can apply the previous property to put the 3 as an exponent in the log

`\sf x(log( {2}^(3) ) + log(8) ) = 2 \\ x( log(8 ) + log(8) ) = 2 \\ 2x log(8) = 2`

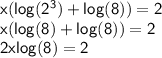
Let's divide both sides by 2 :

`\sf x log(8) =1`

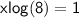
Finally, let's divide both sides by log(8) :

`\boxed{\sf x = (1)/( log(8) ) }`

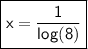
Have a nice day ;)