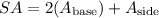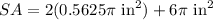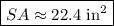Answer the questions below to find the total surface area of the can.

Question

asked Jul 27, 2024 36.8k views

1 Answer

Lazarus Lazaridis · Answer 1 · 2024-07-31T13:49:56+0000

Answer:

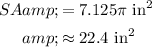
$\begin{aligned}SA &= 7.125\pi \text{ in}^2\\& \approx 22.4 \text{ in}^2 \end{aligned}$

Explanation:

We can find the Surface Area of the can by adding the areas of each of its parts:

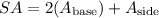
$SA = 2( A_{\text{base}}) + A_\text{side}$

First, we can calculate the area of the circular base:

$A_{\text{circle}} = \pi r^2$

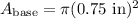
$A_{\text{base}} = \pi (0.75 \text{ in})^2$

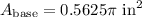
$A_{\text{base}} = 0.5625\pi \text{ in}^2$

Next, we can calculate the area of the rectangular side:

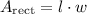
$A_\text{rect} = l \cdot w$

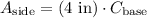
$A_\text{side} = (4\text{ in}) \cdot C_\text{base}$

Since the width of the side is the circumference of the base, we need to calculate that first.

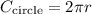
$C_\text{circle} = 2 \pi r$

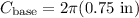
$C_\text{base} = 2 \pi (0.75 \text{ in})$

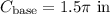
$C_\text{base} = 1.5 \pi \text{ in}$

Now, we can plug that back into the equation for the area of the side:

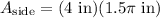
$A_\text{side} = (4\text{ in}) (1.5\pi \text{ in})$

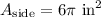
$A_\text{side} = 6\pi \text{ in}^2$

Finally, we can solve for the surface area of the can by adding the area of each of its parts.

$SA = 2( A_{\text{base}}) + A_\text{side}$

$SA = 2(0.5625\pi \text{ in}^2) + 6\pi \text{ in}^2$

$\boxed{SA = 7.125\pi \text{ in}^2}$

$\boxed{SA \approx 22.4 \text{ in}^2}$