Question

. A rope is swinging in such a way that the length of the arc is

decreasing geometrically. If the first arc is 24 feet long and the third

arc is 6 feet long, what is the length of the second arc?

Answer 1

`\huge\boxed{\sf g_2 = 12\ feet}`

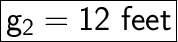
Explanation:

The pattern of the arc:

24, g₂, 6, .....

Since the pattern in decreasing geometrically, we will use the formula:

`a_n=ar^(n-1)`

Where,

n = position of the term

`a_n` = nth term

a = 1st term

r = common ratio (ratio of second to first term)

Solution:

First, we'll find r.

For 3rd term:

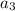`a_3` = 6

a = 24

n = 3

r = ?

So,

`\displaystyle a_3=(24)(r)^(3-1)\\\\6 = 24(r^2)\\\\Divide \ both \ sides \ by \ 24\\\\(6)/(24) = r^2\\\\(1)/(4) = r^2\\\\Take \ square \ root \ on \ both \ sides\\\\(1)/(2) = r\\\\r = (1)/(2)`

Now, to find the second term, we will have to multiply r with the first term.

So,

g₂ = (24) × (1/2)

g₂ = 12

`\rule[225]{224}{2}`