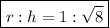Question

24

?
Here is a different solid sphere and a different solid cone.
All measurements are in cm.
The surface area of the sphere is equal to the total surface area of the cone.
(b) Find r:h
Give your answer in the form 1: √n
where n is an integer.

Answer 1

`1 : √(8)`

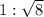
Explanation:

The surface area of a sphere is given by the formula:

`\boxed{S.A._(\sf sphere)=4\pi r^2}`

where r is the radius of the sphere.

The surface area of a cone is the sum of the area of its circular base and the curved area. Therefore:

`\boxed{S.A._(\sf cone)=\pi r^2 + \pi r l}`

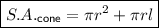
where r is the radius of the base of the cone and
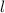`l` is the slant height.

As we need to find the ratio of the radius (r) to the perpendicular height (h) of the cone, we need to rewrite
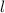`l` in terms of r and h. To do this, we can use Pythagoras Theorem, since r and h are the legs of a right triangle with
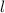`l` as the hypotenuse.

`r^2+h^2=l^2`

`l=√(r^2+h^2)`

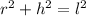
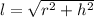
Substitute the expression for
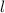`l` into the formula for the equation for the surface area of a cone:

`\boxed{S.A._(\sf cone)=\pi r^2 + \pi r √(h^2+r^2)}`

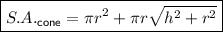
where r is the radius and h is the perpendicular height of the cone.

If the total surface area of the sphere is equal to the total surface area of the cone, then:

`4\pi r^2=\pi r^2 + \pi r √(h^2+r^2)`

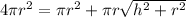
Subtract πr² from both sides of the equation:

`3\pi r^2=\pi r √(h^2+r^2)`

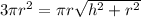
Divide both sides of the equation by πr:

`3r=√(h^2+r^2)`

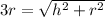
Square both sides of the equation:

`9r^2=h^2+r^2`

Subtract r² from both sides:

`8r^2=h^2`

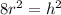
Square root both sides:

`√(8)\;r=h`

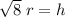
Divide both sides by √8 h:

`(r)/(h)=(1)/(√(8))`

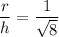
Therefore, the ratio of r : h is:

`\boxed{r : h = 1 : √(8)}`

Answer 2

Let's denote the radius of the sphere by "r" and the height of the cone by "h".

The surface area of the sphere is given by 4πr² and the total surface area of the cone is given by πr√(r² + h²) + πr². We are given that these two are equal, so we can set them equal to each other and solve for r:h.

4πr² = πr√(r² + h²) + πr²

4πr² - πr² = πr√(r² + h²)

3πr² = πr√(r² + h²)

9r⁴ = r²(r² + h²) (squaring both sides)

9r² = r² + h²

8r² = h²

r:h = 1 : √8 = 1 : 2√2 (simplifying the ratio)

Explanation: