Question

use the laplace transform to solve the given system of differential equations. dx dt = −x y dy dt = 2x x(0) = 0, y(0) = 4

Answer 1

`x(t)=(4)/(3)e^t-(4)/(3)e^(-2t)\\ \\y(t)=(4)/(3)e^(-2t)+(8)/(3) e^t}`

Explanation:

Given:

`\left \{ {{x'=-x+y} \atop {y'=2x}} \right.\\\\\text{With initial conditions:} \ x(0)=0 \ \text{and} \ y(0)=4`

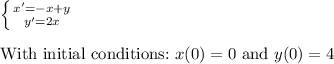
Solve the system of differential equations using Laplace transforms.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

(1) - Take the Laplace transform of each equation

`\boxed{\left\begin{array}{ccc}\text{\underline{Laplace Transforms of DE's:}}\\L\{y''\}=s^2Y-sy(0)-y'(0)\\L\{y'\}=sY-y(0)\\L\{y\}=Y\end{array}\right}`

For equation 1:

`x'=-x+y\\\\\Longrightarrow L\{x'\}=-L\{x\}+L\{y\}\\\\\Longrightarrow sX-0=-X+Y\\\\\Longrightarrow sX=Y-X\\\\\Longrightarrow \boxed{Y=sX+X} \rightarrow \text{Equation 1}`

For equation 2:

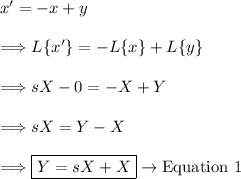
`y'=2x\\\\\Longrightarrow L\{y'\}=2L\{x\}\\\\\Longrightarrow sY-4=2X\\\\\Longrightarrow \boxed{2X=sY-4} \rightarrow \text{Equation 2}`

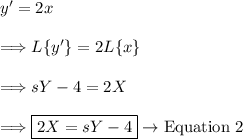
Now we have the following system:

`\left \{ {{Y=sX+X} \atop {2X=sY-4}} \right.`

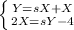
(2) - Solve the system using algebraic techniques (i.e. substitution, elimination, etc..)

`\text{Substituting equation 1 into equation 2: }\\\\\Longrightarrow 2X=s^2X+sX-4\\\\\Longrightarrow s^2X+sX-2X=4\\\\\Longrightarrow X(s^2+s-2)=4\\\\\Longrightarrow \boxed{X=(4)/(s^2+s-2)}`

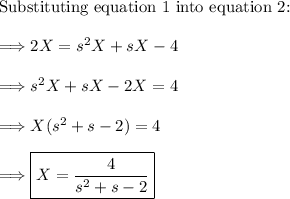
(3) - Take the inverse Laplace transform

`L^(-1)\{X\}=4L^(-1)\{(1)/(s^2+s-2)\}`

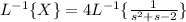
**One the RHS we will have to use partial fraction decomposition to break up the fraction.

`(1)/(s^2+s-2) \Rightarrow (1)/((s-1)(s+2))\\\\\Longrightarrow [(1)/((s-1)(s+2))=(A)/(s-1) +(B)/(s+2)](s-1)(s+2)\\\\\Longrightarrow 1=A(s+2)+B(s-1)\\\\\Longrightarrow 1=As+2A+Bs-B\\\\\Longrightarrow0s+1=(A+B)s+(2A-B)\\\\\Longrightarrow \left \{ {{A+B=0} \atop {2A-B=1}} \right. \\\\\Longrightarrow \text{After solving the system we get:} \ \boxed{A=(1)/(3) \ \text{and} \ B=-(1)/(3) }`

Now we have:

`L^(-1)\{X\}=(4)/(3) L^(-1)\{(1)/(s-1)\}-(4)/(3) L^(-1)\{(1)/(s+2)\}`

`\boxed{\left\begin{array}{ccc}\text{\underline{Table of basic Laplace Transforms:}}\\1\rightarrow (1)/(s) \\t^n\rightarrow (n!)/(s^(n+1))\\e^(at) \rightarrow(1)/(s-a)\\ \sin(at)\rightarrow(a)/(s^2+a^2)\\\cos(at)\rightarrow(s)/(s^2+a^2)\\e^(at)\sin(bt)\rightarrow(b)/((s-a)^2+b^2)\\e^(at)\cos(bt)\rightarrow(s-a)/((s-a)^2+b^2)\\t^ne^(at)\rightarrow(n!)/((s-a)^(n+1)) \end{array}\right}`

`L^(-1)\{X\}=(4)/(3) L^(-1)\{(1)/(s-1)\}-(4)/(3) L^(-1)\{(1)/(s+2)\}\\\\\Longrightarrow \boxed{\boxed{x(t)=(4)/(3)e^t-(4)/(3)e^(-2t)}}`

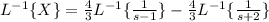
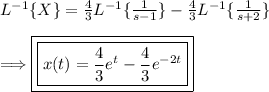
(4) - Repeat steps 2-3 to find y(t)

`\text{Taking equation 2:} \ 2X=sY-4\\\\\Longrightarrow \boxed{X= (sY-4)/(2)} \ \text{Substitute this into equation 1}`

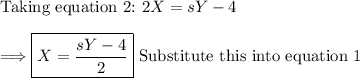
`\Longrightarrow Y=s((sY-4)/(2)})+(sY-4)/(2)}\\\\\Longrightarrow [Y=(s^2Y-4s+sY-4)/(2)]2\\\\\Longrightarrow 2Y=s^2Y-4s+sY-4\\\\\Longrightarrow s^2Y+sY-2Y=4s+4\\\\\Longrightarrow Y(s^2+s-2)=4s+4\\\\\Longrightarrow \boxed{Y= (4s+4)/(s^2+s-2)}`

`L^(-1)\{Y\}=L^(-1)\{(4s+4)/(s^2+s-2)\}\\\\\Longrightarrow 4s+4=A(s-1)+B(s+2)\\\\\Longrightarrow 4s+4=As-A+Bs+2B\\\\\Longrightarrow 4s+4=(A+B)s+(-A+2B)\\\\\Longrightarrow \left \{ {{A+B=4} \atop {-A+2B=4}} \right. \\\\\Longrightarrow A=(4)/(3) \ \text{and} \ B= (8)/(3)`

`L^(-1)\{Y\}=L^(-1)\{(4s+4)/(s^2+s-2)\}\\\\\Longrightarrow L^(-1)\{Y\}=(4)/(3) L^(-1)\{(1)/(s+2) \}+(8)/(3) L^(-1)\{(1)/(s-1) \}\\\\\Longrightarrow \boxed{\boxed{y(t)= (4)/(3)e^(-2t)+(8)/(3) e^t}}`

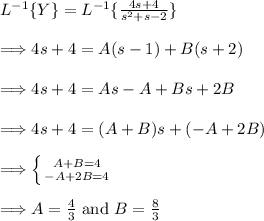
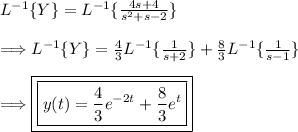
Thus, the system is solved.