Question

An 1,400 kg automobile has springs with k = 1.5 x 10^4 N/m. One of the tires is not properly balanced; it has a little extra mass on one side compared to the other, causing the car to shake at certain speeds.

if the tire radius is 44 cm , at what speed will the wheel shake most?

Answer 1

The speed at which the wheel shakes most is 14.4 m/s (approximately).

The speed at which the wheel shakes most, known as the resonance speed, can be determined by equating the frequency of the bouncing motion to the natural frequency of the system. The natural frequency of a mass-spring system is given by:

`\[ f_{\text{natural}} = (1)/(2\pi) \sqrt{(k)/(m)} \]`

where:

-
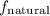`\( f_{\text{natural}} \)` is the natural frequency,

- k is the spring constant,

- m is the mass.

In the case of a wheel shaking, the natural frequency corresponds to the frequency of the bouncing motion. The frequency f is related to the speed v by the formula:

`\[ f = (v)/(2\pi r) \]`

where:

- v is the speed,

- r is the radius of the wheel.

Now, setting the natural frequency equal to the frequency of the bouncing motion, we get:

`\[ (v)/(2\pi r) = (1)/(2\pi) \sqrt{(k)/(m)} \]`

Solving for v, we find:

`\[ v = \sqrt{(k)/(m)} \cdot r \]`

`\[ v = \sqrt{\frac{1.5 * 10^4 \, \text{N/m}}{1400 \, \text{kg}}} \cdot 0.44 \, \text{m} \]`

`\[ v } \]` = 14.4 (approximately)

The value changes with the radius and mass of the automobile.

Answer 2

The speed at which the wheel will shake most is determined as 1.44 m/s.

How to calculate the speed of the wheel?

The speed of the wheel is calculated by applying the following formula as shown below;

ω = √ (k/m)

where;

• m is the mass of the automobile
• k is the spring constant

ω = √ (15000 N/m / 1,400 kg)

ω = 3.27 rad/s

The maximum speed is calculated as;

v = ωr

v = 3.27 rad/s x 0.44 m

v = 1.44 m/s

Thus, the speed at which the wheel will shake most is determined as 1.44 m/s.