Question

A city has two cable companies, X and Y. Each year 20% of the customers using company - move to company Y and 10% of the customers using company Y move to company X. All additional losses and gains of customers by the companies may be ignored. (a) Write down a transition matrix T representing the movements between the two companies in a particular year. (b) Find the eigenvalues and corresponding eigenvectors of T. (c) Hence write down matrices P and D such that T = PDP-¹. Initially company X and company Y both have 1200 customers. (d) Find an expression for the number of customers company X has after n years, where ne N. (e) Hence write down the number of customers that company X can expect to have in the long term.

Answer 1

A student needs assistance calculating a transition matrix for two competing cable companies, finding eigenvalues and eigenvectors, constructing matrices P and D, and determining the number of customers company X has after n years and in the long-term.

Step-by-step explanation:

To address the student's question about the transition matrix and its application to a situation with two competing cable companies, X and Y, we follow a series of steps:

1. First, we define the transition matrix T that represents the movements of customers between the two companies. Company X loses 20% to Company Y, and Company Y loses 10% to Company X, without considering other gains or losses. Therefore, T can be written as:

T = \begin{bmatrix} 0.8 & 0.1 \\ 0.2 & 0.9 \end{bmatrix}

1. We then calculate the eigenvalues and corresponding eigenvectors of matrix T. The eigenvalues are found from the characteristic equation det(T - \lambda I) = 0, and eigenvectors are found using the equation (T - \lambda I)v = 0.
2. Next, we construct matrices P and D such that T = PDP-1, where P contains the eigenvectors and D is a diagonal matrix containing the eigenvalues.
3. For part (d), an expression for the number of customers company X has after n years is found using the equation Xn = TnX0, where X0 is the initial state vector for both companies.
4. Lastly, to find the long-term number of customers for company X, we need to examine the steady state vector, which is the limit of TnX0 as n approaches infinity.

It's important to note that in long-term, the system will reach an equilibrium where the proportion of customers between the two companies becomes constant.

Answer 2

(a) The transition matrix
`\( T \)` representing the movements between the two cable companies X and Y is given by:

`\[ T = \begin{bmatrix} 0.8 & 0.1 \\ 0.2 & 0.9 \end{bmatrix} \]`

(b) The eigenvalues of
`\( T \)` are 0.7 and 1. The corresponding eigenvectors are
`\([1, -1]\)` for the eigenvalue 0.7 and
`\([1, 2]\)` for the eigenvalue 1.

(c) The matrices
`\( P \) and \( D \)` can be constructed as follows:

`\[ P = \begin{bmatrix} 1 & 1 \\ -1 & 2 \end{bmatrix} \]`

`\[ D = \begin{bmatrix} 0.7 & 0 \\ 0 & 1 \end{bmatrix} \]`

such that
`\( T = PDP^(-1) \).`

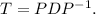
Step-by-step explanation:

(a) The transition matrix
`\( T \)` is constructed based on the given information about the movements of customers between the two cable companies. The entries represent the probabilities of transitioning from one company to the other.

(b) To find the eigenvalues, we solve the characteristic equation
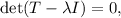`\( \text{det}(T - \lambda I) = 0 \),` where
`\( I \)` is the identity matrix. The corresponding eigenvectors are then found by substituting each eigenvalue back into
`\( (T - \lambda I)\mathbf{v} = \mathbf{0} \).`

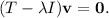
(c) The matrices
`\( P \) and \( D \)` are obtained by arranging the eigenvectors into
`\( P \)` and the eigenvalues into
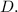`\( D \).` The relationship
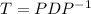`\( T = PDP^(-1) \)` is a diagonalization of the transition matrix
`\( T \).`

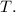
In conclusion, the calculations provide the necessary matrices
`\( P \) and \( D \)` for the diagonalization of
`\( T \)`. These matrices are crucial for analyzing the long-term behavior of the customer movements between the two cable companies, as described in the subsequent parts of the question.