Answer:
Convergent
Explanation:
One method to determine if
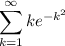 is convergent or divergent is the Integral Test.
is convergent or divergent is the Integral Test.
Suppose that the function we use is
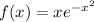 . Over the interval
. Over the interval
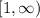 , the function is always positive and continuous, but we also need to make sure it is decreasing before we can proceed with the Integral Test.
, the function is always positive and continuous, but we also need to make sure it is decreasing before we can proceed with the Integral Test.
The derivative of this function is
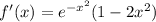 , so our critical points will be
, so our critical points will be
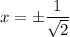 , but we can drop the negative critical point as we are starting at
, but we can drop the negative critical point as we are starting at
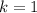 . Using some test points, we can see that the function increases on the interval
. Using some test points, we can see that the function increases on the interval
![\bigr[0,(1)/(√(2))\bigr]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7yf23n79ui2n7zy1t7e88djgk7pmp1xt3f.png) and decreases on the interval
and decreases on the interval
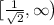 . Since the function will eventually decrease, we can go ahead with the Integral Test:
. Since the function will eventually decrease, we can go ahead with the Integral Test:
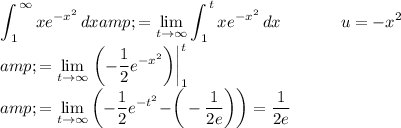
Therefore, since the integral is convergent, the series must also be convergent by the Integral Test.