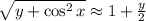Question

Find the linear approximation of the given function at (0, 0). f(x, y).

f (x, y)= √ (y +cos (x)^2

Answer 1

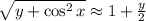`√(y+\cos^2x)\approx 1+(y)/(2)` at (0,0)

Explanation:

The linear approximation of a function
`f(x,y)` at a given point
`(x_0,y_0)` is given by the equation:

`f(x,y)\approx f(x_0,y_0)+(\partial f)/(\partial x)_((x_0,y_0))(x-x_0)+(\partial f)/(\partial y)_((x_0,y_0))(y-y_0)`

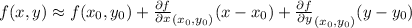
Find f(0,0)

`f(x,y) = √(y+\cos^2x)`

`f(0,0)=√(0+\cos^20)=√(0+1)=√(1)=1`

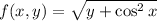
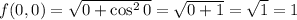
Determine ∂f/∂x and ∂f/∂y at (0,0)

`\displaystyle (\partial f)/(\partial x)_((0,0))=(-\sin x\cos x)/(√(y+\cos^2x))=(-\sin0\cos0)/(√(0+\cos^20))=0 \\\\(\partial f)/(\partial y)_((0,0))=(1)/(2√(y+\cos^2x))=(1)/(2√(0+\cos^20))=(1)/(2)`

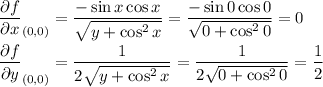
Plug the above values into the linear approximation equation

`f(x,y)\approx f(0,0)+(\partial f)/(\partial x)_((0,0))(x-0)+(\partial f)/(\partial y)_((0,0))(y-0)\\√(y+\cos^2x)\approx 1+0x+(1)/(2)y\\√(y+\cos^2x)\approx 1+(y)/(2)`

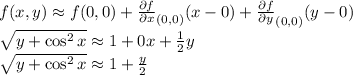
Therefore, the linear approximation of the given function at (0,0) is
`√(y+\cos^2x)\approx 1+(y)/(2)`