Question

Give the equation of a circle with a diameter that has endpoints (-7, 7) and (3, 6).

Answer 1

(x + 2)^2 + (y - 6.5)^2 = 25.25

Explanation:

We can the equation of the circle in standard form, whose general equation is:

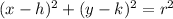`(x-h)^2+(y-k)^2=r^2`, where

• (h, k) are the coordinates of the circle's center,
• and r is the radius

Step 1: We know that the diameter is simply 2 * the radius. Thus, we can find the radius by first finding the length of the diameter. To do this, we'll need the distance formula, which is:

`d=\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2 }`, where

• (x1, y1) is one coordinate,
• and (x2, y2) is the other coordinate.

We can allow (-7, 7) to be our (x1, y1) and (3, 6) to be our (x2, y2) point and plug these into the formula to find d, the distance between the points and the length of the diameter:

`d=√((3-(-7))^2+(6-7)^2) \\d=√((3+7)^2+(-1)^2)\\ d=√((10)^2+1)\\ d=√(100+1)\\ d=√(101)`

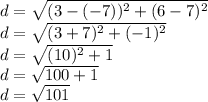
Now we can multiply our diameter by 1/2 to find the length of the radius:

r = 1/2√101

Step 2: We know that the center lies at the middle of the circle and therefore represents the midpoint of the diameter. The midpoint formula is

`m=((x_(1)+x_(2) )/(2)),((y_(1)+y_(2) )/(2))`, where

• (x1, y1) is one coordinate,
• and (x2, y2) is another coordinate

We can allow (-7, 7) to be our (x1, y1) point and (3, 6) to be our (x2, y2) point:

`m=((-7+3)/(2)),((7+6)/(2))\\ m=((-4)/(2)),((13)/(2))\\ m=(-2,6.5)`

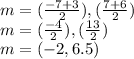
Thus, the coordinate for the center are (-2, 6.5).

Step 3: Now, we can create the equation of the circle and simplify:

(x - (-2)^2 + (y - 6.5)^2 = (1/2√101)^2

(x + 2)^2 + (y - 6.5)^2 = 25.25