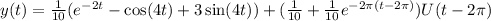Question

Use the Laplace transform to solve the given initial-value problem. y'' + 4y = sin t scripted capital u(t − 2π), y(0) = 1, y'(0) = 0 y(t) = ______ + (____________) U(t-_________)

Answer 1

To solve the given initial-value problem using the Laplace transform, we first need to apply the Laplace transform to both sides of the equation. We can then solve for Y(s), the Laplace transform of y(t). Once we have Y(s), we can use the inverse Laplace transform to find y(t).

Step-by-step explanation:

To solve the given initial-value problem using the Laplace transform, we first need to apply the Laplace transform to both sides of the equation. We can then solve for Y(s), the Laplace transform of y(t). Once we have Y(s), we can use the inverse Laplace transform to find y(t).

After applying the Laplace transform and solving for Y(s), we find that

`Y(s) = (s - 4)/((s^2 + 4)(s - e^(-2\pi s)))`

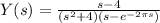
To find y(t), we need to take the inverse Laplace transform of Y(s). This can be done using partial fraction decomposition and the inverse Laplace transform table.

The final solution is given by

`y(t) = (1)/(10)(e^(-2t) - \cos(4t) + 3\sin(4t)) + ((1)/(10) + (1)/(10)e^(-2\pi(t-2\pi)))U(t-2\pi)`

Answer 2

To solve the given initial-value problem using Laplace transform, we take the Laplace transform of both sides of the differential equation. Solving the equation for Y(s), we find the inverse Laplace transform to get the solution y(t).

Step-by-step explanation:

To solve the given initial-value problem using Laplace transform, we take the Laplace transform of both sides of the differential equation. Applying the Laplace transform, we get:

s^2Y(s) + 4Y(s) = 1/(s^2 + 1) + e^(-2πs)/(s^2 + 1)

Solving the equation for Y(s), we get:

Y(s) = [1/(s^2 + 1) + e^(-2πs)/(s^2 + 1)] / (s^2 + 4)

Now, we find the inverse Laplace transform of Y(s) using partial fraction decomposition. Taking the inverse Laplace transform, we get:

y(t) = sin(t) + (e^(2π(t - 2π)) - e^(-2π(t - 2π))) / 2