1. The tension in the string connecting the two blocks
 is approximately
is approximately
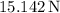
2. The tension in the string tied to the wall
 is approximately \
is approximately \
 .
.
How to find the tension?
Given:
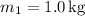 (mass of the lower block)
(mass of the lower block)
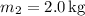 (mass of the upper block)
(mass of the upper block)
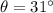 (angle of the incline)
(angle of the incline)
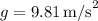 (acceleration due to gravity)
(acceleration due to gravity)
For Block 2 (2.0 kg):
Using Newton's second law
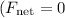 as the acceleration is zero):
as the acceleration is zero):
![\[2 m_2 g \sin(\theta) + T_2 - T_1 = 0\]](https://img.qammunity.org/2024/formulas/physics/high-school/5jpntq67q32pfoutq3e80k781z0noa557b.png)
![\[2 m_2 g \sin(\theta) + T_2 = T_1\] ...(1)](https://img.qammunity.org/2024/formulas/physics/high-school/7xt9ocs571wtvb97x98y7099osebmnqvgf.png)
For Block 1 (1.0 kg):
![\[T_2 = m_1 g \sin(\theta)\] ...(2)](https://img.qammunity.org/2024/formulas/physics/high-school/kf9sg7wpwjgw2btbp9gkoy1w65u4f921mw.png)
Substitute equation (2) into equation (1):
![\[2 m_2 g \sin(\theta) + m_1 g \sin(\theta) = T_1\]](https://img.qammunity.org/2024/formulas/physics/high-school/7twz7kdro3oa9g25ty8alnkh79bebboycd.png)
![\[3 m_1 g \sin(\theta) = T_1\]](https://img.qammunity.org/2024/formulas/physics/high-school/8o0l1oqa7t7hrzlzkx3zsfzuscfuikz1cx.png)
![\[3 * 1 * 9.81 * \sin(31\textdegree) \approx 15.142 \, \text{N}\]](https://img.qammunity.org/2024/formulas/physics/high-school/m95mp7ujf1ixlofyb9r6punx8w5fzt4s36.png)
Therefore, the tension in the string connecting the two blocks
 is approximately
is approximately
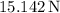 .
.
Now, for
 :
:
![\[T_2 = m_1 g \sin(\theta)\]](https://img.qammunity.org/2024/formulas/physics/high-school/6fguvaswyli53zua1vgxhkjs2gldu25rzd.png)
![\[1 * 9.81 * \sin(31\textdegree) \approx 5.04 \, \text{N}\]](https://img.qammunity.org/2024/formulas/physics/high-school/u5obx0m0hytvg3gda4yraql1iadvfcp74s.png)
Therefore, the tension in the string tied to the wall
 is approximately
is approximately
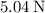 .
.