Question

If side a measures 30 feet and side b measures 40 feet, how many feet of flowers will be planted along side c, the hypotenuse of the triangle? Show your work.

Answer 1

Answer: Here, side a = 30ft.

side b = 40ft.

Hence according to, Pythagoras theorem,

h²=p²+b²

where, h= hypotenuse of the triangle

b= base of the triangle

p= perpendicular of the triangle

Explanation:

hypotenuse c {according to question} - c=
`\sqrt{a^(2) + b^(2)`

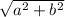
therefore, c=
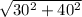`\sqrt{30^(2) + 40^(2) }` = 50ft. will be the answer.

Hypotenuse means the longest side of the triangle or in other words the side opposite to the 90° angle of the triangle.

Answer 2

You dont have to tell me to show my work twice

Explanation:

To find the length of side c (the hypotenuse), we will use the Pythagorean theorem, which states that in a right triangle, the sum of the squares of the two shorter sides (a and b) is equal to the square of the hypotenuse (c).

In this case, a = 30 feet and b = 40 feet. Therefore:

c^2 = a^2 + b^2

c^2 = 30^2 + 40^2

c^2 = 900 + 1600

c^2 = 2500

c = √2500

c = 50 feet

So the length of side c (the hypotenuse) is 50 feet. To find out how many feet of flowers will be planted along side c, we need to know the perimeter of the triangle (the sum of the lengths of all three sides). The perimeter is:

Perimeter = a + b + c

Perimeter = 30 + 40 + 50

Perimeter = 120 feet

Therefore, 120 feet of flowers will be planted along side c.