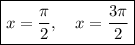Question

PreCalc- Solving Trigonometric Equations

Can anyone explain the steps, I have the answer but doesn’t throughly explain how.

Answer 1

`x=(\pi)/(2),\quad x=(3\pi)/(2)`

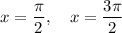
Explanation:

Given trigonometric equation:

`\boxed{2\cos^2(x) \csc(x)-\cos^2(x)=0}`

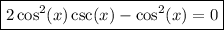
To solve the equation, begin by factoring out cos²(x) from the left side of the equation:

`\cos^2(x) \left(2\csc(x)-1\right)=0`

Apply the zero-product property to create two equations to solve:

`\cos^2(x)=0\quad \textsf{and} \quad 2\csc(x)-1=0`

`\hrulefill`

Solve cos²(x) = 0:

`\begin{aligned}\cos^2(x)&=0\\\\√(\cos^2(x))&=√(0)\\\\\cos(x)&=0\\\\x&=(\pi)/(2)+2\pi n, (3\pi)/(2)+2\pi n\end{aligned}`

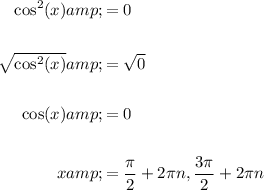
[To find the solutions using a unit circle, locate the points where the x-coordinate is zero, since each (x, y) point on the unit circle is equal to (cos θ, sin θ).]

Therefore, the solutions on the interval [0, 2π] are:

`x=(\pi)/(2),\; (3\pi)/(2)`

`\hrulefill`

Solve 2csc(x) - 1 = 0:

`\begin{aligned}2 \csc(x)-1&=0\\\\2\csc(x)&=1\\\\\csc(x)&=(1)/(2)\\\\(1)/(\sin(x))&=(1)/(2)\\\\\sin(x)&=2\end{aligned}`

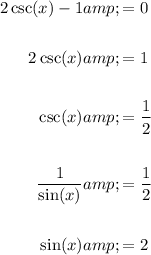
As the range of the sine function is -1 ≤ sin(x) ≤ 1, there is no solution for x ∈ R.

`\hrulefill`

Solutions

Therefore, the solutions to the given trigonometric equation on the interval [0, 2π] are:

`\boxed{x=(\pi)/(2),\quad x=(3\pi)/(2)}`