Question

For the following equation:

2x^2-50=0
(1) Calculate the discriminant
(2) Determine the number and type of solutions
(3) Use the quadratic formula to solve

Answer 1

(1) Discriminant = 400

(2) There are two real solutions

(3) x = 5 and x = -5

Explanation:

(1)

2x^2 - 50 = 0 is in standard form, whose general equation is

ax^2 + bx + c.

From the equation, we see that

• 2 is our a value,
• 0 is our b value,
• and -50 is our c value.

The discriminant comes from the quadratic formula and is given by:

b^2 - 4ac

Thus, we can find the discriminant of the given equation by plugging in 0 for b, 2 for a, and -50 for c and simplifying:

0^2 - 4(2)(-50)

0 + 400

400

Thus, the discriminant is 400:

(2)

• When the discriminant (b^2 - 4ac) < 0, there are 0 real solutions and either one or two complex solutions
• When the discriminant (b^2 - 4ac) = 0, there is 1 real solution
• When the discriminant (b^2 - 4ac) > 0, there are 2 real solutions

Because our discriminant 400 > 0, there are two real solutions (two being the number of solutions and real signifying the type)

(3)

The quadratic formula is

`x=(-b+/-√(b^2-4ac) )/(2a)`

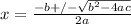
• the +/- comes from the fact that when you take the square root, you get a positive and negative result,
• and x is the root or solution to the quadratic.

We know that our equation has two solutions. Let's find the positive solution first and then the negative one. For both solutions, we must plug in 2 for a, 0 for b, and -50 for c:

Positive solution:

`x=(-0+√(0^2-4(2)(-50)) )/(2(2))\\ \\x=(√(400) )/(4)\\ \\x=(20)/(4)\\ \\x=5`

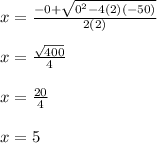
Negative solution:

`x=(-0-√(0^2-4(2)(-50)) )/(2(2))\\ \\x=(-√(400) )/(4)\\ \\x=(-20)/(4)\\ \\x=-5`

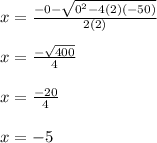
We can check that we've found the correct solutions by seeing whether we get 0 when we plug in 5 for x and -5 for x into the equation:

Plugging in 5 for x:

2(5)^2 - 50 = 0

2(25) - 50 = 0

50 - 50 = 0

0 = 0

Plugging in -5 for x:

2(-5)^2 - 50 = 0

2(25) - 50 = 0

50 - 50 = 0

0 = 0