Question

A cone has a volume of 15,225pi cubic mm. what is the radius of the base if the height is 203 mm?

Answer 1

Radius = 15 mm

Explanation:

As you've written, the formula for volume of a cone is

V = 1/3πr^2h, where

• V is the volume in cubic units,
• r is the radius,
• and h is the height.

Step 1: First, we can rewrite the formula in terms of radius by multiplying both sides by 3, dividing both sides by πh, and lastly by taking the square root of both sides:

`3(V=1/3\pi r^2h)\\(3V=\pi r^2h)/\pi h\\√((3V/\pi h))=r`

Step 2: Now we can plug in 15225π for V and 203 for h to solve for r, the radius:

`\sqrt{(((3(15225\pi)) )/((203\pi ))) } =r\\\\\sqrt{(((45675\pi) )/((203\pi ))) }=r\\ \\√(225)=r\\ \\15=r\\-15=r`

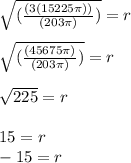
Although a square root always has a positive and negative answer, we can only use the positive answer, since you can't have a negative measure. Thus, the measure of the radius is 15 mm.

Optional Step 3: We can check that we've correctly found the right radius by plugging in 15 for r in the regular volume formula and seeing whether we get 15225π on both sides:

15225π = 1/3π * 15^2 * 203

15225π = 1/3π * 225 * 203

15225π = 1/3π * 45675

15225π = 15225π

Answer 2

The radius of the base is 15 mm.