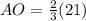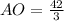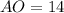Question

In the figure below, ⎯⎯⎯⎯⎯⎯⎯⎯,⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯,

B
L
¯
,
A
M
¯
,
and ⎯⎯⎯⎯⎯⎯⎯⎯⎯
C
K
¯
are medians of △
△
A
B
C
. If AM = 21 and LO = 4, then AO =

Answer 1

AO = 14

Explanation:

The figure we are given shows the intersection of the medians of this triangle. In fact, the point of intersection of the medians is called the centroid. In this problem, O is the centroid.

The intersection of the medians of a triangle has some properties:

(1) The distance from a vertex of the triangle to the centroid is 2/3 of the distance from said vertex to the opposite side of the vertex

(2) The distance from the centroid to a side opposite of a vertex is 1/3 of the distance from said vertex to the opposite side of said vertex

(3) The longer part of the median partitioned by the centroid is twice the distance of the shorter part of said median partitioned by the centroid

We can use the first property stated to find the distance of AO.

`AO = (2)/(3) AM`

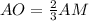
We are given that AM = 21

`AO = (2)/(3)(21)`

`AO = (42)/(3)`

`AO = 14`