Question

A triangle has sides with lengths of 12 miles, 84 miles, and 85 miles. Is it a right triangle?

Answer 1

Ggggggghhhhggffggtfgugggh

Answer 2

`\boxed {\boxed {\sf No}}`

Explanation:

If a triangle is a right triangle, it can satisfy Pythagorean Theorem.

`a^2+b^2=c^2`

where a and b are the legs and c is the hypotenuse.

12 and 84 are the legs because are they shortest. 85 is the hypotenuse because it is the longest side.

`a= 12 \\b=84 \\c=85`

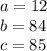
Substitute the values into the formula.

`(12)^2+(84)^2=(85)^2`

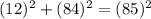
Solve the exponents.

• 12²= 12*12=144
• 84²=84*84=7056
• 85²= 85*85=7225

`144+7056=7225`

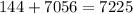
Add on the right side.

`7200\\eq 7225`

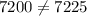
7220 is not equal to 7225, so these sides cannot be a right triangle.