Question

|x + 3 | = 4x - 3
which of your answers is extraneous....

Answer 1

`D:4x-3\geq0\\D:4x\geq3\\D:x\geq(3)/(4)\\\\|x + 3 | = 4x - 3\\x+3=4x-3 \vee x+3=-4x+3\\3x=6 \vee 5x=0\\x=2 \vee x=0`

`0\\ot\geq(3)/(4)` therefore, that's the extraneous solution.

Answer 2

The valid solution is x = 2.

The extraneous solution is x = 0.

Explanation:

The bars either side of an expression or a value are the absolute value symbol. "Absolute value" means how far a value is from zero. Therefore, the absolute value of a number is its positive numerical value.

To solve an equation containing an absolute value, first isolate the absolute value on one side of the equation. (Note: This has already been done).

`|x + 3 | = 4x - 3`

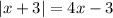
Next, set the contents of the absolute value equal to both the positive and negative value of the expression on the other side of the equation.

`\underline{\sf Case\;1\;(positive)}\\\\x+3=4x-3`

`\underline{\sf Case\;2\;(negative)}\\\\x+3=-(4x-3)`

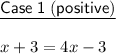
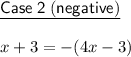
Solve both equations for x.

`\underline{\sf Case\;1\;(positive)}\\\\\begin{aligned}x+3&=4x-3\\-3x&=-6\\x&=2\end{aligned}`

`\underline{\sf Case\;2\;(negative)}\\\\\begin{aligned}x+3&=-(4x-3)\\x+3&=-4x+3\\5x&=0\\x&=0\end{aligned}`

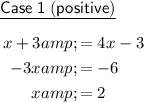
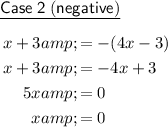
So the two potential solutions are x = 2 and x = 0.

An extraneous solution is a solution that is produced by solving the problem, but is not a valid solution to the problem.

Check if any of these solutions are extraneous by substituting them back into the original equation:

`\begin{aligned}\textsf{For $x=2$:} \quad |2 + 3| &= 4(2) - 3\\|5| &= 8 - 3\\5 &= 5\;\;\; \sf(True)\end{aligned}`

`\begin{aligned}\textsf{For $x=0$:} \quad |2 + 3| &= 4(0) - 3\\|5| &= 0 - 3\\5 &= -3\;\;\; \sf(False)\end{aligned}`

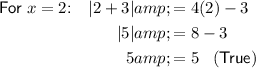
Therefore, the only valid solution is x = 2, and the extraneous solution is x = 0.