Question

Find the center and radius of the circle given by this equation: 22 - 10x + y? + 6y - 30 = 0

Answer 1

Explanation:

By further evaluating your question, I concluded based on my observation that the equation you asked must be this one:

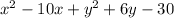`x^(2) -10x + y^(2) +6y -30` = 0 or
`x^(2) -10x + y^(2) +6y = 30`

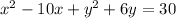
by completing the square formula of the x and y, you can get the center point of the circle

(1)
`[x^(2) -10x+25] +[y^(2) +6y+9] = 30 + 25 + 9`

(2)
`(x-5)^(2) +(y+3)^(2) = 64`

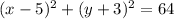
this would give us the center point of (5,-3) and the radius of 8 units.

Area =
`\pi x 8^2`

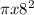
Area = 200.96 sq. units