Question

What is the cube root of 512?​

Answer 1

8

Step-by-step explanation:

Since 512 is a perfect cube, we will use the prime factorization method to get the cube root.

Step 1: Find the prime factors of 512.

512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2

Step 2: Pair the factors of 512 in a group of three, such that they form cubes.

512 = (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2)

512 = 2³ × 2³ × 2³

Using the law of exponents, we get;

512 =
`2^(3+3+3)` =
`2^(9)` [
`a^(m)` ×
`a^(n)` =
`a^(m + n)`]

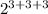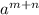So,

512 = 8³

Step 3: Now, we will apply cube root on both sides to take out the factor (in cubes) as a single term.

3√512 = 3√(83)

So, here the cube root is eliminated by the cube of 8.

Hence, 3√512 = 8