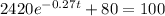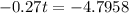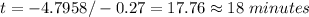Question

A welder drops a piece of red-hot steel on the floor. The initial temperature of the steel is 2,500 degrees Fahrenheit. The ambient temperature is 80 degrees Fahrenheit. After 2 minutes the temperature of the steel is 1,500 degrees. The function f(t)=Ce(−kt)+80 represents the situation, where t is time in minutes, C is a constant, and k is a constant.

After 2 minutes the temperature of the steel is 1,500 degrees. After how many minutes will the temperature of the steel be 100 degrees and therefore safe to pick up with bare hands? Round your answer to the nearest whole number, and do not include units.

Answer 1

18 minutes rounded to nearest integer

Explanation:

The relation between the temperature of steel in °F and time elapsed is

`f(t) = C e^(-kt) + 80`

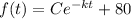
where
t is in minutes, C and k are constants

At time t = 0, f(t) = 2500

Plugging these values into the expression:

`f(0) = C e^(-k\cdot 0) + 80\\\\e*{-k\cdot0} = e^(0) = 1\\\\f(0) = C \cdot 1 + 80 = 2500\\C = 2500-80 = 2420`

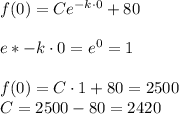
Therefore,

`f(t) = 2420 e^(-kt) + 80`

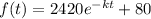
Temperature after 2 minutes = 1500 °F

Plugging these values into the function we get

`2420 \cdot e^(-2k) + 80 = 1500\\\\2420 \cdot e^(-2k) = 1500 - 80 = 1420\\ \\e^(-2k) = (1420)/(2420)\\\\`

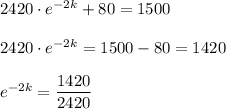
Taking natural logs on both sides:

`ln(e^(-2k))} = \ln\left((1420)/(2420)}\right)`

`-2k = -0.53311 \quad\quad \text{since $ln(e^x) = x$}`

`k = -0.266555 \approx -0.27`

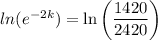
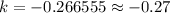
The function therefore is

`f(t) = 2420 e^(-0.27t) + 80`

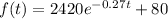
to find out how many minutes it will take for the temperature to be 100 degrees we substitute 100 for f(t) and solve for t

`2420 e^(-0.27t) + 80 = 100`

`-0.27t = \ln{(20)/(2420)}`

`-0.27t = -4.7958`

`t = -4.7958/-0.27 = 17.76 \approx 18\; minutes`