Question

If csc θ = ‒2, what is the value of sin θ?

Answer 1

sin(θ) =
`-(1)/(2)`

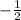
Explanation:

The trigonometric identities all relate to each in unique ways.

Sin and Csc

Sin and csc, aka sine and cosecant, are reciprocals. This means that cosecant =
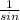`(1)/(sin)` and sine =
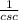`(1)/(csc)`. This means that given the value of csc, all we need to do is take the reciprocal. This will give us the value of sin.

• 
  `\displaystyle (1)/(csc)` =
  `-(1)/(2)`

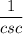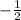
The reciprocal of -2 is -1/2, so sin θ = -1/2.

Other Reciprocal Values

Sin and Csc are not the only reciprocal trigonometric identities. The reciprocal of cosine is secant (cos and sec). Additionally, the reciprocal of tangent is cotangent (tan and cot). Furthermore, all of these identities can be related to each other using the Pythagorean identity:

• sin²θ + cos²θ = 1

All of these facts help us better understand and use trigonometry.