Question

A 175.0 g uniform meter stick used as a balance has masses 325.0 g at the 90.0 cm position and 200.0 at the 25.0 cm position. Where should the meter stick be pivoted so the system is balanced? a. 65.2 cm b. 65.2 cm c. 72.9 cm d. 61.4 cm

Answer 1

To find the pivot point where the system is balanced, set up an equation of torques by considering the masses and distances from the pivot point. In this case, the meter stick should be pivoted at approximately 72.9 cm.

Step-by-step explanation:

To find the pivot point where the system is balanced, we need to consider the torques acting on the meter stick. The torques due to the masses can be calculated by multiplying the mass of each object by its distance from the pivot point. Since the meter stick is uniform, its weight can be considered to act at its center of mass. By setting up an equation of torques, we can solve for the pivot point. In this case, the meter stick should be pivoted at approximately 72.9 cm to achieve balance.

Answer 2

The correct answer is approximately
`\( x \approx 65.2 \, \text{cm} \).`

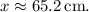
To find the pivot point where the meter stick is balanced, we can use the principle of torques. The torque (τ) is given by the formula:

`\[ \tau = F \cdot r \]`

where F is the force applied, and r is the distance from the pivot point to the point where the force is applied.

For the system to be balanced, the sum of torques on one side of the pivot point must equal the sum of torques on the other side.

Let's denote the pivot point as x (in cm). The torques on the left side (counterclockwise) must equal the torques on the right side (clockwise). The torques are calculated by multiplying the force by the distance.

The torques on the left side:

`\[ \tau_{\text{left}} = (200.0 \, \text{g}) \cdot (x - 25.0 \, \text{cm}) \]`

The torques on the right side:

`\[ \tau_{\text{right}} = (325.0 \, \text{g}) \cdot (90.0 \, \text{cm} - x) \]`

For balance,
`\(\tau_{\text{left}}\) must equal \(\tau_{\text{right}}\):`

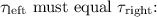
`\[ (200.0 \, \text{g}) \cdot (x - 25.0 \, \text{cm}) = (325.0 \, \text{g}) \cdot (90.0 \, \text{cm} - x) \]`

Now, solve for x:

`\[ 200x - 5000 = 325 \cdot 90 - 325x \]`

`\[ 200x + 325x = 325 \cdot 90 + 5000 \]`

`\[ 525x = 29250 + 5000 \]`

`\[ 525x = 34250 \]`

`\[ x = (34250)/(525) \]`

Now, calculate x:

`\[ x \approx 65.24 \, \text{cm} \]`