Question

Let F(x,y,z)=yi^+xj^+z2k^ be a vector field. Determine if its conservative, and find a potential if it is.

Answer 1

The vector field is conservative and its potential function is
`\bold{f(x,y,z)=xy+(1)/(3)z^3 +C}`

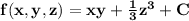
Step-by-step explanation:

Given the vector field
`\vec F(x,y,z)=y\hat i+x \hat j +z^2 \hat k`. Determine whether or not it is conservative and if so find the potential function.

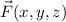`\vec F(x,y,z)` is said to be conservative if the
`curl\vec F = < 0,0,0 >`.

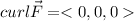To find the
`curl \vec F`...

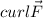`curl \vec F=\left[\begin{array}{ccc}\hat i&\hat j&\hat k\\dx&dy&dz\\P&Q&R\end{array}\right]\\\\ P=y \\\\ Q=x \\\\ R=z^2`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`curl \vec F=\left[\begin{array}{ccc}\hat i&\hat j&\hat k\\dx&dy&dz\\y&x&z^2\end{array}\right]\\\\=[(z^2)(dy)-(x)(dz)]\hat i-[(z^2)(dx)-(y)(dz)]\hat j+[(x)(dx)-(y)(dy)]\hat k\\\\=[0-0]\hat i-[0-0]\hat j+[1-1]\hat k\\\\=0\hat i-0\hat j+0\hat k \Longrightarrow \boxed{curl\vec F= < 0,0,0 > \therefore Conservative}`

The vector field is conservative. Now we must find its potential function. Follow these steps to find the potential function.

Integrating the P term with respect to x:

`\int\ {P} \, dx \Longrightarrow \int\ {y} \, dx \Longrightarrow \boxed{=xy}`

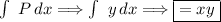
Integrating the Q term with respect to y:

`\int\ {Q} \, dy \Longrightarrow \int\ {x} \, dy \Longrightarrow \boxed{=xy}`

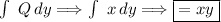
Integrating the R term with respect to z:

`\int\ {R} \, dz \Longrightarrow \int\ {z^2} \, dz \Longrightarrow \boxed{=(1)/(3) z^3}`

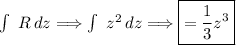
The potential function is made up of the results of the above integrals ignoring any repeat terms.

`\boxed{f(x,y,z)=xy+(1)/(3)z^3 +C}`

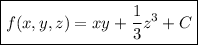
Thus, the problem is solved.