Question

APPLICATION

3. Use the first principle of derivatives to determine the equation of tangent to the
curve y = 1/radical7x at
x = 5

Answer 1

`\displaystyle y - (√(35))/(35) = (-√(35))/(350)(x - 5)`

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

Coordinates (x, y)

Point-Slope Form: y - y₁ = m(x - x₁)

• x₁ - x coordinate
• y₁ - y coordinate
• m - slope

Algebra II

• Exponential Rule [Rewrite]:
  `\displaystyle b^(-m) = (1)/(b^m)`

Calculus

Derivatives

• The definition of a derivative is the slope of the tangent line.

Derivative Notation

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Chain Rule:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Explanation:

Step 1: Define

`\displaystyle y = (1)/(√(7x)) \\x = 5`

Step 2: Differentiate

1. [Function] Rewrite:
   `\displaystyle y = (1)/((7x)^(1)/(2))`
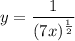
2. [Function] Rewrite [Exponential Rule - Rewrite]:
   `\displaystyle y = (7x)^{-(1)/(2)}`
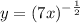
3. [Derivative] Chain Rule [Function]:
   `\displaystyle y' = (-1)/(2)(7x)^{-(1)/(2) - 1} \cdot (d)/(dx)[7x]`
4. [Derivative] Simplify:
   `\displaystyle y' = (-1)/(2)(7x)^{-(3)/(2)} \cdot (d)/(dx)[7x]`
5. [Derivative] Basic Power Rule:
   `\displaystyle y' = (-1)/(2)(7x)^{-(3)/(2)} \cdot 1 \cdot 7x^(1 - 1)`
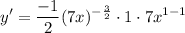
6. [Derivative] Simplify:
   `\displaystyle y' = (-7)/(2)(7x)^{-(3)/(2)}`
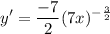
7. [Derivative] Rewrite [Exponential Rule - Rewrite]:
   `\displaystyle y' = \frac{-7}{2(7x)^{(3)/(2)}}`

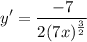
Step 3: Find Slope of Tangent Line

1. Substitute in x [Derivative]:
   `\displaystyle y'(5) = \frac{-7}{2[7(5)]^{(3)/(2)}}`
2. [Tangent Slope] [Brackets] Multiply:
   `\displaystyle y'(5) = \frac{-7}{2[35]^{(3)/(2)}}`
3. [Tangent Slope] Evaluate exponents:
   `\displaystyle y'(5) = (-7)/(2(35√(35)))`
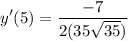
4. [Tangent Slope] Multiply:
   `\displaystyle y'(5) = (-7)/(70√(35))`
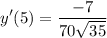
5. [Tangent Slope] Simplify:
   `\displaystyle y'(5) = (-1)/(10√(35))`
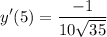
6. [Tangent Slope] Rationalize:
   `\displaystyle y'(5) = (-√(35))/(350)`

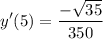
Step 4: Find Tangent Line Equation

Point (x, y)

1. Substitute in x [Function]:
   `\displaystyle y(5) = (1)/(√(7(5)))`
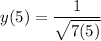
2. [Function] [√Radical] Multiply:
   `\displaystyle y(5) = (1)/(√(35))`
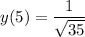
3. [Function] Rationalize:
   `\displaystyle y(5) = (√(35))/(35)`
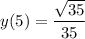
4. Define point:
   `\displaystyle (5, (√(35))/(35))`

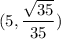
Equation

1. Substitute in variables [Point-Slope Form]:
   `\displaystyle y - (√(35))/(35) = (-√(35))/(350)(x - 5)`

Topic: AP Calculus AB/BC

Unit: Derivatives

Book: College Calculus 10e