Question

. Air entrainment is a process of entrapping tiny air bubbles in concrete mix in order to increase the durability of the hardened concrete in freeze-thaw climates. After 35 days, the breaking stress [in psi] was measured for concrete samples with and without air entrainment. Based on the data, does the air entrainment process increase the breaking stress of the concrete

Answer 1

This question is incomplete, the complete question is;

Air entrainment is a process of entrapping tiny air bubbles in concrete mix in order to increase the durability of the hardened concrete in freeze-thaw climates. After 35 days, the breaking stress [in psi] was measured for concrete samples with and without air entrainment. Based on the data, does the air entrainment process increase the breaking stress of the concrete. { ∝ = 0.05 }, assuming population variances are equal.

Air Entrainment No Air Entrainment

4479 4118

4436 4531

4358 4315

4724 4237

4414 3888

4358 4279

4487 4311

3984

4197

4327

Answer:

Since p-value ( 0.088) > significance level ( 0.05)

hence, Failed to reject Null hypothesis

It is then concluded that the null hypothesis H₀ is NOT REJECTED.

Therefore, there is no sufficient evidence to claim that population mean μ1 is greater than μ2 at 0.05 significance level.

We conclude that Air entrainment process can't increase the breaking stress of the concrete.

Step-by-step explanation:

Given the data in the question;

mean x" = (4479 + 4436 + 4358 + 4724 + 4414 + 4358 + 4487 + 3984 + 4197 + 4327) / 10

mean x"1 = 43764 / 10 = 4376.4

x ( x - x" ) ( x - x" )²

4479 102.6 10526.76

4436 59.6 3552.16

4358 -18.4 338.56

4724 347.6 120825.76

4414 37.6 1413.76

4358 -18.4 338.56

4487 110.6 12232.36

3984 -382.4 153977.76

4197 -179.4 32184.36

4327 -49.4 2440.36

∑ 337830.4

Standard deviation s1 = √( (∑( x - x" )²) / n -1

Standard deviation s1 = √( 337830.4 / (10 - 1 ))

Standard deviation s1 = 193.74

x2 ( x2 - x"2 ) ( x2 - x"2 )²

4118 -121.9 14859.61

4531 291.1 84739.21

4315 75.1 5640.01

4237 -2.9 8.41

3888 -351.9 123833.61

4279 39.1 1528.81

4311 71.1 5055.21

∑ 235664.87

mean x"2 = (4118 + 4531 + 4315 + 4237 + 3888 + 4279 + 4311) / 7

mean x"2 = 29679 / 7 = 4239.9

Standard deviation s2 = √( (∑( x2 - x" )²) / n2 - 1

Standard deviation s1 = √( 337830.4 / (7 - 1 ))

Standard deviation s1 = 198.19

so

Mean x"1 = 4376.4, S.D1 = 193.74, n1 = 10

Mean x"2 = 4239.9, S.D2 = 198.19, n2 = 7

so;

Null Hypothesis H₀ : μ1 = μ2

Alternative Hypothesis H₁ : μ1 > μ2

Lets determine our rejection region;

based on the data provided. the significance level ∝ = 0.005

with degree of freedom DF = n1 + n2 - 2 = 10 + 7 - 2 = 15

so, Critical Value = 1.753

The rejection region for this right -tailed is R = t:t > 1.753

Test statistics

since it is assumed that the population variances are equal, so we calculate pooled standard deviation;

Sp = √{ [ (n1 -1)S.D1² + (n2 - 1)S.D2²] / [ n1 + n2 -2 ]

we substitute

Sp = √{ [ (10 -1)(193.74)² + (7 - 1)(198.19)²] / [ 10 + 7 -2 ]

Sp = √ [ 573492.345 / 15 ]

Sp = 195.53

so the Test statistics will be;

t = (x"1 - x"2) / Sp√(
`(1)/(n1)` +
`(1)/(n2)` )

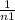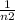t = (4376.4 - 4239.9) / 195.53√(
`(1)/(10)` +
`(1)/(7)` )

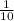t = 136.5 / 96.36

t = 1.42

so

P-value = 0.088

Since p-value ( 0.088) > significance level ( 0.05)

hence, Failed to reject Null hypothesis

It is then concluded that the null hypothesis H₀ is NOT REJECTED.

Therefore, there is no sufficient evidence to claim that population mean μ1 is greater than μ2 at 0.05 significance level.

We conclude that Air entrainment process can't increase the breaking stress of the concrete.