Question

The position of a ball after it is launched in the air can be determined by using the function f(x) =

-0.9x^2 + 2.7x + 3.5 where f(x) is the height of the ball, in feet, above the ground and x is the horizontal distance, in feet, from the point at which it was launched.

a) What is the height of the ball when it is launched?

b) What is the highest point of the ball in the air?

c) How far is the ball horizontally from its starting position when it reaches its highest height?

Answer 1

a) 3.5 feet

b) 5.525 feet

c) 1.5 feet

Explanation:

a) Easy: Just look at the constant term of the function.

b) Given that f(x) is in the form ax²+bx+c, where a=-0.9, b=2.7, and c=3.5...

Use x = (-b)/(2a) = (-2.7)/(2*-0.9) = 1.5 to find the x-coordinate of the

maximum point (vertex). Then substitute that value in for x:

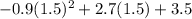`-0.9(1.5)^(2) +2.7(1.5)+3.5\\`. Use the Order of Operations to correctly

evaluate:
`=-0.9(2.25)+2.7(1.5)+3.5=-2.025+4.05+3.5=`.

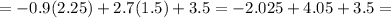c) Already calculated as the x-coordinate in (b).