Question

1. Isosceles Triangle The two equal sides of an isosceles triangle are each 42

centimeters. If the base measures 30 centimeters, find the height and the

measure of the two equal angles. Round your answer to the nearest tenth.

Answer 1

1. H = 29 cm

2. θ = 44°

Explanation:

1. We can find the height of the triangle by considering the isosceles triangle as two right triangles. The height can be found by using Pitagoras:

`L^(2) = H^(2) + B^(2)`

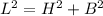
Where:

L: is the sides of the isosceles triangle = 42 cm

B: is the base = 30 cm

H: is the height =?

Then, the height is:

`H = \sqrt{L^(2) - B^(2)} = \sqrt{(42 cm)^(2) - (30 cm)^(2)} = 29.4 cm = 29 cm`

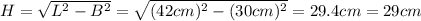
2. The two equal angles (θ) can be found using the following trigonometric identity:

`cos(\theta) = (B)/(L)`

`\theta = cos^(-1)((30 cm)/(42 cm)) = 44.4^(\circ) = 44^(\circ)`

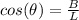
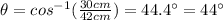
Hence, the two equal angles are 44°.

I hope it helps you!