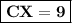Question

HELP!!! Solve for x

Answer 1

1) x = 5

2) x = 9

3) CX = 9

Explanation:

1) Tangents from an external point to circle are equal length.

AB = AD

5x - 4 = 3x + 6

Add 4 to both the sides,

5x = 3x + 6 + 4

5x = 3x + 10

Subtract 3x from both sides,

5x - 3x = 10

2x = 10

Divide both sides by 2,

x = 10 ÷ 2

`\boxed{\bf x = 5}`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~`

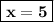
2) Tangent of the circle is perpendicular to the radius the circle at the point of contact. So, ΔADC is a right-angle triangle. To find x, we can use Pythagorean theorem.

AC = AB + BC

AC = 6 + x

Pythagorean theorem,

AC² = DC² + DA²

(x + 6)² = x² + 12²

x² + 12x + 36 = x² + 144 {Identity: (a +b)² = a² + 2ab + b²}

12x + 36 = x² + 144 - x²

12x + 36 = 144

Subtract 36 from both sides,

12x = 144 - 36

12x = 108

Divide both sides by 12,

x = 108 ÷ 12

`\boxed{\bf x = 9}`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

3) Pythagorean theorem,

CX² + XB² = BC²

CX² + 12² = 15²

CX² + 144 = 225

Subtract 144 from both sides,

CX² = 225 - 144

CX² = 81

Take square root,

CX= √81

`\boxed{\bf CX = 9}`