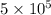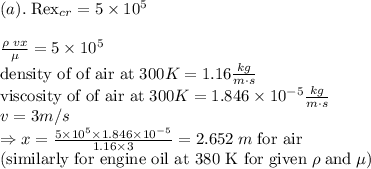Given:
Assuming the transition to turbulence for flow over a flat plate happens at a Reynolds number of 5x105, determine the following for air at 300 K and engine oil at 380 K. Assume the free stream velocity is 3 m/s.
To Find:
a. The distance from the leading edge at which the transition will occur.
b. Expressions for the momentum and thermal boundary layer thicknesses as a function of x for a laminar boundary layer
c. Which fluid has a higher heat transfer
Calculation:
The transition from the lamina to turbulent begins when the critical Reynolds
number reaches