Answer:
At t=2s the car reach its minimum speed
Minimum speed=8m/s
Explanation:
We are given that velocity of car
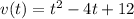
0<t<4
Differentiate w.r.t t
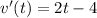
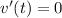
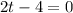
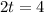
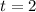
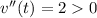
The velocity is minimum at t=2 s
Substitute t=2

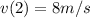
Hence, the speed of car is minimum at t=2 se and minimum speed of car=8m/s